
| A. | $\frac{625}{6}$ | B. | $\frac{250}{6}$ | C. | $\frac{375}{6}$ | D. | $\frac{125}{6}$ |
分析 由题意,先根据二项展开式的通项求出常数项m,然后利用积分,求得图形的面积即可
解答 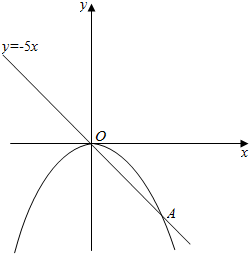 解:由于(x-$\frac{1}{x}$)6的展开式的通项为Tr+1=$(-1)^{r}{C}_{6}^{r}{x}^{6-2r}$,
解:由于(x-$\frac{1}{x}$)6的展开式的通项为Tr+1=$(-1)^{r}{C}_{6}^{r}{x}^{6-2r}$,
分别令6-2r=0可得r=3,T4=-20,
令6-2r=-1,则r不存在,
令6-2r=-2可得r=4,T5=15x-2,
∴m=-20×1+15x-2×x2=-5,
∴y=-x2与y=mx=-5x的交点O(0,0),A(5,-25),
图象围成的封闭图形的面积S=${∫}_{0}^{5}(-{x}^{2}+5x)dx$=$(-\frac{1}{3}{x}^{3}+\frac{5}{2}{x}^{2}){|}_{0}^{5}$=$\frac{125}{6}$.
故选:D.
点评 本题考查定积分在求面积中的应用以及二项式的性质,求解的关键利用二项式定理求出常数项,积分与二项式定理这样结合,形式较新颖,本题易因为对两个知识点不熟悉公式用错而导致错误,牢固掌握好基础知识很重要.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪(0,1] | B. | (-∞,-1]∪[0,1] | C. | (0,1] | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | ±3 | C. | $±\sqrt{2}$ | D. | ±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
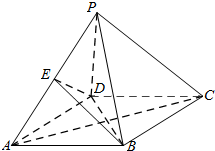 如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\sqrt{10}$ | D. | $\frac{2\sqrt{390}}{39}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com