练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=
    		x-1
    的单调递增区间为
     
    ．
    考点：函数单调性的判断与证明
    专题：函数的性质及应用
    分析：先求出函数的定义域，再根据复合函数“同增异减”的性质，从而求出函数的单调区间．
    解答： 解：∵x-1≥0，
    ∴函数的定义域是：[1，+∞），
    又y=
    		x
    ，y=x-1同为增函数，
    ∴y=
    		x-1
    在定义域单调递增，
    故答案为：[1，+∞）．
    点评：本题考查了复合函数的单调性，考查了二次函数的定义域，是一道基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

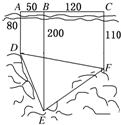    如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知AB=50m，BC=120m，于A处测得水深AD=80m，于B处测得水深BE=200m，于C处测得水深CF=110m，则∠DEF的余弦值为（　　）
    A、
    16
    65
    B、
    19
    65
    C、
    16
    57
    D、
    17
    57

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=（
    1
    2
    ） x2+2(a-1)x+2在区间（-∞，4]上单调递增，那么实数a的取值范围是（　　）
    A、a≤-3B、a≥-3
    C、a≤5D、a≥5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

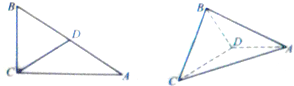    在Rt△ABC中，BC=2，AB=4，∠ACB=90°，D为边AB的中点，沿CD把△BCD折起，使平面BCD⊥平面ACD．
    （1）求异面直线BC与AD所成角的余弦值．
    （2）求平面ABC与平面ABD所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a=3-
    1
    3
    ，b=log2
    1
    3
    ，c=log
    1
    2
    1
    3
    ，则（　　）
    A、a＞b＞c
    B、a＞c＞b
    C、c＞a＞b
    D、c＞b＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    《中华人民共和国个人所得税》规定，全民全月工资、薪金所得不超过1600元的不必纳税，超过1600元的部分为全月应纳税所得额．此项税款按下表分段累计计算：
    全民应纳税所得额税率（%）
    不超过500元的部分5
    超过500元至2000元的部分10
    超过2000元至5000元的部分15
    超过5000元至20000元的部分20
    超过20000元至40000元的部分25
    超过40000元至60000元的部分30
    超过60000元至80000元的部分35
    超过80000元至100000元的部分40
    超过100000元的部分45
    某人出版了一书共纳税420元，这个人的稿费为
     
    元．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设an（n=2，3，4，…）是（2+x）n的展开式中x2项的系数，则
    2010
    2009
    ×（
    22
    a2
    +
    23
    a3
    +
    24
    a4
    +…+
    22010
    a2010
    ）=（　　）
    A、8B、4C、2D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    二项式（x2-
    1
    x
    ）9的展开式中的常数项为（　　）
    A、36B、-36
    C、84D、-84

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知ab=8，alog2b=4，求a、b的值．

    查看答案和解析>>

    同步练习册答案