
(10分)如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,
现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?

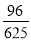
【解析】
试题分析:几何概型的特点:一是无限性,即在一次试验中,基本事件个数可以使无限的;二是等可能性,
即每个事件发生的可能性相等.对于一个具体问题能否应用几何概型概率公式,关键在于能否将问题几何
化;也可以根据实际问题的具体情况,选择合适的参数,建立适当的坐标系。在此基础上,将试验每一个
结果一一对应于该坐标系的每一个点,使得全体结果构成一个可度量的区域
试题解析:因为均匀的粒子落在正方形内任何一点是等可能的,所以符合几何概型的条件。设A=“粒子落在中间带形区域”则依题意得正方形面积为:25×25=625,两个等腰直角三角形的面积为:2×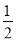 ×23×23=529,带形区域的面积为:625-529=96,所以P(A)=
×23×23=529,带形区域的面积为:625-529=96,所以P(A)= 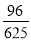
考点:几何概型问题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源:2014-2015学年河南省郑州市高一第一次月考数学试卷(解析版) 题型:选择题
下列各组函数是同一函数的是( )
①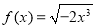 与
与 ;
;
② 与
与 ;
;
③ 与
与 ;
;
④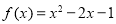 与
与 。
。
A.①② B.①③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省郑州市高二10月月考数学试卷(解析版) 题型:选择题
如图,圆C内切于扇形AOB, 若在扇形AOB内任取一点,则该点在圆C内的概率为( )
若在扇形AOB内任取一点,则该点在圆C内的概率为( )

A、 B、
B、 C、
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省郑州市高二10月月考数学试卷(解析版) 题型:选择题
把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是( )
(A)对立事件 (B)互斥但不对立事件
(C)不可能事件 (D)必然事件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省郑州市高一10月月考数学试卷(解析版) 题型:选择题
已知函数 f(x)=x5+ax3+bx-8 ,且 f(-2)=10,那么f(2)等于( )
A. -10 B.-18 C.-26 D.10
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省洛阳市高一10月月考数学试卷(解析版) 题型:解答题
(本题18分)某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com