
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获最大利润?最大利润有多大?
每天应生产A 型桌子2 张,B 型桌子3 张,才能获最大利润, 最大利润为13千元.
【解析】
试题分析:先设每天生产甲型桌子x张,乙型桌子y张,利润总额为z元,根据题意抽象出x,y满足的条件,建立约束条件,作出可行域,再根据目标函数z═2x+3y,利用截距模型,平移直线找到最优解即可.
解:设每天生产A型桌子x张,B型桌子y张,每天所获利润为z千元,
依题意,得
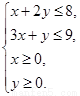
目标函数为 ,
,
如图,作出可行域,
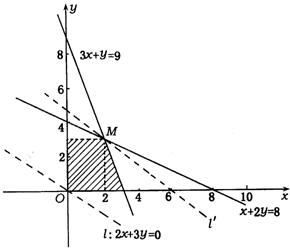
由z =2 x +3 y,得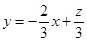 ,
,
把直线l: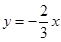 向右上方平移至
向右上方平移至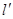 位置时,
位置时,
直线经过可行域上的点M,且与原点距离最大.
由 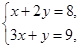 得
得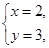 ∴
∴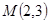 ,
,
∴ 直线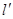 的方程为
的方程为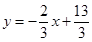 ,
,
∴ 当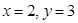 时,
时,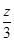 取最大值
取最大值 ,即z取最大值13,
,即z取最大值13,
答:每天应生产A 型桌子2 张,B 型桌子3 张,才能获最大利润, 最大利润为13千元.
考点:本试题主要考查了用线性规划解决实际问题中的最值问题,基本思路是抽象约束条件,作出可行域,利用目标函数的类型,找到最优解.属中档题
点评:解决该试题的关键是可行域的求解以及目标函数的斜率与已知线性约束条件中斜率的关系是解决中的一个重要的细节。


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下学期期末数学试卷(解析版) 题型:解答题
(12分)某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源:2014届福建漳州市下学期高一期中数学试卷(解析版) 题型:填空题
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,现设工厂每天应生产A、B型桌子分别为 张,则
张,则 应满足的约束条件
应满足的约束条件
是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com