Question

已知如图，斜三棱柱ABC—A₁B₁C₁的侧面A₁ACC₁与底面ABC垂直，∠ABC＝90°，BC＝2，AC＝2，且AA₁⊥A₁C，AA₁＝A₁C.

（Ⅰ）求侧棱A₁A与底面ABC所成角的大小；

（Ⅱ）求侧面A₁ABB₁与底面ABC所成二面角的大小；

（Ⅲ）求顶点C到侧面A₁ABB₁的距离.

Answer 1

答案：
解析：

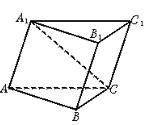
解：（Ⅰ）作A1D⊥AC，垂足为D，由面A1ACC1⊥面ABC，得A1D⊥面ABC ∴∠A1AD为A1A与面ABC所成的角. ∵AA1⊥A1C，AA1＝A1C， ∴∠A1AD＝45°为所求. （Ⅱ）作DE⊥AB，垂足为E，连A1E，则由A1D⊥面ABC，得A1E⊥AB， ∴∠A1ED是面A1ABB1与面ABC所成二面角的平面角. 由已知，AB⊥BC，得ED∥BC. 又D是AC的中点，BC＝2，AC＝2， ∴DE＝1，AD＝A1D＝， tanA1ED＝． 故∠A1ED＝60°为所求. （Ⅲ）解法一：由点C作平面A1ABB1的垂线，垂足为H，则CH的长是C到平面A1ABB1的距离. 连结HB，由于AB⊥BC，得AB⊥HB. 又A1E⊥AB，知HB∥A1E，且BC∥ED， ∴∠HBC＝∠A1ED＝60°. ∴CH＝BCsin60°＝为所求. 解法二：连结A1B. 根据定义，点C到面A1ABB1的距离，即为三棱锥C—A1AB的高h. 由， 即. ∴h＝为所求.