
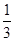 ax3+
ax3+ x2+(a-1)x-
x2+(a-1)x-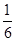 (x>0),(aÎR).
(x>0),(aÎR). 时,讨论f (x)的单调性;
时,讨论f (x)的单调性; 时,f (x)在(0,1),(
时,f (x)在(0,1),(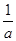 -1,+¥)递减;在(1,
-1,+¥)递减;在(1, 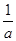 -1)递增
-1)递增 )∪(
)∪( ,1).
,1).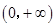 .
.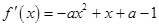 =-a(x-1)[x-(
=-a(x-1)[x-(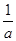 -1)]. ……2分
-1)]. ……2分 时,
时,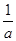 -1>1,
-1>1,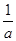 -1,+¥)递减;在(1,
-1,+¥)递减;在(1, 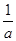 -1)递增; ……4分
-1)递增; ……4分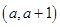 上不具有单调性等价于f (x)在区间
上不具有单调性等价于f (x)在区间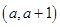 内至少有一个极值点. ……5分
内至少有一个极值点. ……5分 时,f ¢(x)=-
时,f ¢(x)=- (x-1)2≤0Þf (x)在
(x-1)2≤0Þf (x)在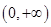 上递减,不合题意; …7分
上递减,不合题意; …7分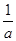 -1,∵
-1,∵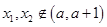 ,故不合题意;③当
,故不合题意;③当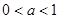 ,且a≠
,且a≠ 时,f (x)在区间
时,f (x)在区间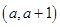 上不具有单调性等价于:
上不具有单调性等价于: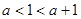 或
或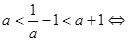
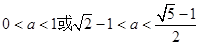
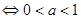
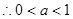 ,且a≠
,且a≠ . ……11分
. ……11分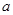 的取值范围是(0,
的取值范围是(0, )∪(
)∪( ,1). ……12分
,1). ……12分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com