证明:任意0<x
1<x
2,
∵

,
∵0<x
1<x
2,
∴x
1-x
2<0,x
1x
2>0,
∴

<0,即f(x
1)<f(x
2),
∴f(x)在(0,+∞)上为增函数.
分析:利用单调性的定义来证明函数是一个单调函数,先设出任意两个正数变量,表明它们的大小关系,对两个变量对应的函数值做差,合并同类项,通分整理,最终形式是变化为因式的积或商的形式,这样就可以根据条件判断差和零的关系,得到结论.
点评:本题考查函数单调性的证明,考查对于代数式的整理,是一个基础题,这种题目经常考到,可以作为一个解答题目的一问出现,这种题目的证法一般只有两种,一是用定义,二是用导数.

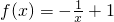 在区间(0,+∞)上是单调增函数.
在区间(0,+∞)上是单调增函数.