
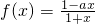 x2
x2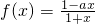 x2,
x2,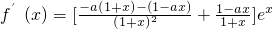
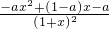 ex,
ex,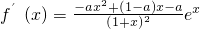 ,(x>0)
,(x>0)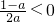 ,
, .
. 时,g(x)=0有两个不等的实根x1,x2,设x1<x2,
时,g(x)=0有两个不等的实根x1,x2,设x1<x2,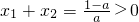 ,
,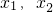 )上大于0,
)上大于0,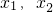 )上为增函数,
)上为增函数,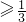 时,△=(1-a)2-4a2≤0,
时,△=(1-a)2-4a2≤0,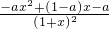 ex,由已知f′(0)=-1,能求出a.
ex,由已知f′(0)=-1,能求出a.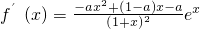 ,(x>0)令g(x)=-ax2+(1-a)x-a,则f′(x)与g(x)的符号相同.由此进行分类讨论,能够推导出当a≤0时,对任意x>0,恒有f(x)>1.
,(x>0)令g(x)=-ax2+(1-a)x-a,则f′(x)与g(x)的符号相同.由此进行分类讨论,能够推导出当a≤0时,对任意x>0,恒有f(x)>1.

科目:高中数学 来源: 题型:解答题
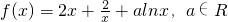 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省青岛市胶州一中高三(上)期末数学试卷(文科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东师大附中高三(上)12月月考数学试卷(文科)(解析版) 题型:解答题
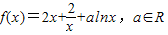 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
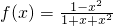 .
.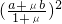 ]-f(
]-f(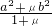 )≥
)≥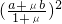 -
-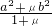 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com