
ЁОЬтФПЁПвЛПюЛїЙФаЁгЮЯЗЕФЙцдђШчЯТЃКУПХЬгЮЯЗЖМашвЊЛїЙФШ§ДЮЃЌУПДЮЛїЙФвЊУДГіЯжвЛДЮвєРжЃЌвЊУДВЛГіЯжвєРжЃКУПХЬгЮЯЗЛїЙФШ§ДЮКѓЃЌГіЯжвЛДЮвєРжЛёЕУ10ЗжЃЌГіЯжСНДЮвєРжЛёЕУ20ЗжЃЌГіЯжШ§ДЮвєРжЛёЕУ100ЗжЃЌУЛгаГіЯжвєРждђПлГ§200ЗжЃЈМДЛёЕУЉ200ЗжЃЉЃЎЩшУПДЮЛїЙФГіЯжвєРжЕФИХТЪЮЊ ![]() ЃЌЧвИїДЮЛїЙФГіЯжвєРжЯрЛЅЖРСЂЃЎ
ЃЌЧвИїДЮЛїЙФГіЯжвєРжЯрЛЅЖРСЂЃЎ
ЃЈ1ЃЉЩшУПХЬгЮЯЗЛёЕУЕФЗжЪ§ЮЊXЃЌЧѓXЕФЗжВМСаЃЛ
ЃЈ2ЃЉЭцШ§ХЬгЮЯЗЃЌжСЩйгавЛХЬГіЯжвєРжЕФИХТЪЪЧЖрЩйЃП
ЃЈ3ЃЉЭцЙ§етПюгЮЯЗЕФаэЖрШЫЖМЗЂЯжЃЎШєИЩХЬгЮЯЗКѓЃЌгызюГѕЗжЪ§ЯрБШЃЌЗжЪ§УЛгадіМгЗДЖјМѕЩйСЫЃЎЧыдЫгУИХТЪЭГМЦЕФЯрЙижЊЪЖЗжЮіЗжЪ§МѕЩйЕФдвђЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКXПЩФмШЁжЕгаЉ200ЃЌ10ЃЌ20ЃЌ100ЃЎ
дђPЃЈX=Љ200ЃЉ= ![]() ЃЌ
ЃЌ
PЃЈX=10ЃЉ= ![]() =
= ![]()
PЃЈX=20ЃЉ= ![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=100ЃЉ= ![]() =
= ![]() ЃЌ
ЃЌ
ЙЪЗжВМСаЮЊЃК
X | Љ200 | 10 | 20 | 100 |
P |
|
|
|
|
гЩЃЈ1ЃЉжЊЃЌУПХЬгЮЯЗГіЯжвєРжЕФИХТЪЪЧp= ![]() +
+ ![]() =
= ![]()
ЃЈ2ЃЉНтЃКдђжСЩйгавЛХЬГіЯжвєРжЕФИХТЪp=1Љ ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉНтЃКгЩЃЈ1ЃЉжЊЃЌУПХЬгЮЯЗЛёЕУЕФЗжЪ§ЮЊXЕФЪ§бЇЦкЭћЪЧEЃЈXЃЉ=ЃЈЉ200ЃЉЁС ![]() +10ЁС
+10ЁС ![]() +20ЁС
+20ЁС ![]() ЁС100=Љ
ЁС100=Љ ![]() =
= ![]() ЃЎ
ЃЎ
етЫЕУїУПХЬгЮЯЗЦНОљЕУЗжЪЧИКЗжЃЌгЩИХТЪЭГМЦЕФЯрЙижЊЪЖПЩжЊЃКаэЖрШЫОЙ§ШєИЩХЬгЮЯЗКѓЃЌШызюГѕЕФЗжЪ§ЯрБШЃЌЗжЪ§УЛгадіМгЗДЖјЛсМѕЩйЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЩшУПХЬгЮЯЗЛёЕУЕФЗжЪ§ЮЊXЃЌЧѓГіЖдгІЕФИХТЪЃЌМДПЩЧѓXЕФЗжВМСаЃЛЃЈ2ЃЉЧѓГігавЛХЬГіЯжвєРжЕФИХТЪЃЌЖРСЂжиИДЪдбщЕФИХТЪЙЋЪНМДПЩЕУЕННсТлЃЎЃЈ3ЃЉМЦЫуГіЫцЛњБфСПЕФЦкЭћЃЌИљОнЭГМЦгыИХТЪЕФжЊЪЖНјааЗжЮіМДПЩЃЎ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫРыЩЂаЭЫцЛњБфСПМАЦфЗжВМСаЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮедкЩфЛїЁЂВњЦЗМьбщЕШР§згжаЃЌЖдгкЫцЛњБфСПXПЩФмШЁЕФжЕЃЌЮвУЧПЩвдАДвЛЖЈДЮађвЛвЛСаГіЃЌетбљЕФЫцЛњБфСПНазіРыЩЂаЭЫцЛњБфСПЃЎРыЩЂаЭЫцЛњБфСПЕФЗжВМСаЃКвЛАуЕФ,ЩшРыЩЂаЭЫцЛњБфСПXПЩФмШЁЕФжЕЮЊx1,x2,.....,xi,......,xnЃЌXШЁУПвЛИіжЕ xi(i=1,2,......ЃЉЕФИХТЪP(ІЮ=xiЃЉЃНPiЃЌдђГЦБэЮЊРыЩЂаЭЫцЛњБфСПX ЕФИХТЪЗжВМЃЌМђГЦЗжВМСаВХФме§ШЗНтД№ДЫЬтЃЎ


 ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвджБНЧзјБъЯЕЕФдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсЃЌЧвСНИізјБъЯЕШЁЯрЕШЕФГЄЖШЕЅЮЛНЈСЂзјБъЯЕ.вбжЊжБЯп
жсЕФе§АыжсЮЊМЋжсЃЌЧвСНИізјБъЯЕШЁЯрЕШЕФГЄЖШЕЅЮЛНЈСЂзјБъЯЕ.вбжЊжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЧњЯп
ЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉ.
ЮЊВЮЪ§ЃЉ.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭжБЯп
ЕФЦеЭЈЗНГЬКЭжБЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉжБЯп![]() ЩЯгавЛЕу
ЩЯгавЛЕу![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() гыЧњЯп
гыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌPAЁЭЕзУцABCDЃЌADЁЭABЃЌABЁЮDCЃЌAD=DC=AP=2ЃЌAB=1ЃЌЕуEЮЊРтPCЕФжаЕуЃЎ 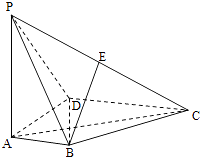
ЃЈ1ЃЉжЄУїЃКBEЁЭDCЃЛ
ЃЈ2ЃЉЧѓжБЯпBEгыЦНУцPBDЫљГЩНЧЕФе§ЯвжЕЃЛ
ЃЈ3ЃЉШєFЮЊРтPCЩЯвЛЕуЃЌТњзуBFЁЭACЃЌЧѓЖўУцНЧFЉABЉPЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаУќЬтЃК
ЂйДцдкЪЕЪ§![]() ,ЪЙ
,ЪЙ![]() ЃЛ ЂкКЏЪ§
ЃЛ ЂкКЏЪ§![]() ЪЧХМКЏЪ§ЃЛ
ЪЧХМКЏЪ§ЃЛ
ЂлШє![]() ЪЧЕквЛЯѓЯоЕФНЧЃЌЧв
ЪЧЕквЛЯѓЯоЕФНЧЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂмжБЯп![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФвЛЬѕЖдГЦжсЃЛ
ЕФвЛЬѕЖдГЦжсЃЛ
ЂнКЏЪ§![]() ЕФЭМЯёЙигкЕу
ЕФЭМЯёЙигкЕу![]() ГЩЖдГЦжааФЭМаЮ.
ГЩЖдГЦжааФЭМаЮ.
Цфжае§ШЗУќЬтЕФађКХЪЧ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=sinЃЈ3x+ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓfЃЈxЃЉЕФЕЅЕїЕндіЧјМфЃЛ
ЃЈ2ЃЉШєІСЪЧЕкЖўЯѓЯоНЧЃЌfЃЈ ![]() ЃЉ=
ЃЉ= ![]() cosЃЈІС+
cosЃЈІС+ ![]() ЃЉcos2ІСЃЌЧѓcosІСЉsinІСЕФжЕЃЎ
ЃЉcos2ІСЃЌЧѓcosІСЉsinІСЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМзЁЂввСНИіТУгЮОАЕужЎМфгавЛЬѕ5kmЕФжБЯпаЭЫЎТЗЃЌвЛЫвгЮТжвд![]() ЕФЫйЖШКНааЪБ
ЕФЫйЖШКНааЪБ![]() ПМТЧЕНКНЯпАВШЋвЊЧѓ
ПМТЧЕНКНЯпАВШЋвЊЧѓ![]() ЃЌУПаЁЪБЪЙгУЕФШМСЯЗбгУЮЊ
ЃЌУПаЁЪБЪЙгУЕФШМСЯЗбгУЮЊ![]() ЭђдЊ
ЭђдЊ![]() ЮЊГЃЪ§ЃЌЧв
ЮЊГЃЪ§ЃЌЧв![]() ЃЌЦфЫћЗбгУЮЊУПаЁЪБ
ЃЌЦфЫћЗбгУЮЊУПаЁЪБ![]() ЭђдЊЃЎ
ЭђдЊЃЎ
![]() ШєгЮТжвд
ШєгЮТжвд![]() ЕФЫйЖШКНааЪБЃЌУПаЁЪБЪЙгУЕФШМСЯЗбгУЮЊ
ЕФЫйЖШКНааЪБЃЌУПаЁЪБЪЙгУЕФШМСЯЗбгУЮЊ![]() ЭђдЊЃЌвЊЪЙУПаЁЪБЕФЫљгаЗбгУВЛГЌЙ§
ЭђдЊЃЌвЊЪЙУПаЁЪБЕФЫљгаЗбгУВЛГЌЙ§![]() ЭђдЊЃЌЧѓxЕФШЁжЕЗЖЮЇЃЛ
ЭђдЊЃЌЧѓxЕФШЁжЕЗЖЮЇЃЛ
![]() ЧѓИУгЮТжЕЅГЬКНааЫљашзмЗбгУЕФзюаЁжЕЃЎ
ЧѓИУгЮТжЕЅГЬКНааЫљашзмЗбгУЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊP1ЃЈa1 ЃЌ b1ЃЉгыP2ЃЈa2 ЃЌ b2ЃЉЪЧжБЯпy=kx+1ЃЈkЮЊГЃЪ§ЃЉЩЯСНИіВЛЭЌЕФЕуЃЌдђЙигкxКЭyЕФЗНГЬзщ ![]() ЕФНтЕФЧщПіЪЧЃЈ ЃЉ
ЕФНтЕФЧщПіЪЧЃЈ ЃЉ
A.ЮоТлkЃЌP1 ЃЌ P2ШчКЮЃЌзмЪЧЮоНт
B.ЮоТлkЃЌP1 ЃЌ P2ШчКЮЃЌзмгаЮЈвЛНт
C.ДцдкkЃЌP1 ЃЌ P2 ЃЌ ЪЙжЎЧЁгаСННт
D.ДцдкkЃЌP1 ЃЌ P2 ЃЌ ЪЙжЎгаЮоЧюЖрНт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњФЯББГЏЪБЦкЕФжјзїЁЖЫязгЫуОЁЗжаЃЌЖдЭЌгрГ§ЗЈгаНЯЩюЕФбаОПЃЎЩш![]()
ЮЊећЪ§ЃЌШє![]() КЭ
КЭ![]() БЛ
БЛ![]() Г§ЕУЕФгрЪ§ЯрЭЌЃЌдђГЦ
Г§ЕУЕФгрЪ§ЯрЭЌЃЌдђГЦ![]() КЭ
КЭ![]() ЖдФЃ
ЖдФЃ![]() ЭЌгрЃЌМЧЮЊ
ЭЌгрЃЌМЧЮЊ![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕПЩвдЪЧ
ЕФжЕПЩвдЪЧ
A. 2015 B. 2016 C. 2017 D. 2018
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() ЃЌЕу
ЃЌЕу![]() ЪЧдВ
ЪЧдВ![]() ЩЯШЮвтвЛЕуЃЌЯпЖЮ
ЩЯШЮвтвЛЕуЃЌЯпЖЮ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дкдВЩЯдЫЖЏЪБЃЌЕу
дкдВЩЯдЫЖЏЪБЃЌЕу![]() ЕФЙьМЃЮЊЧњЯп
ЕФЙьМЃЮЊЧњЯп![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() гыЧњЯп
гыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌ
СНЕуЃЌ![]() ЮЊзјБъдЕуЃЌЧѓ
ЮЊзјБъдЕуЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЃЎ
УцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com