
过点(1,0)的直线与中心在原点,焦点在x轴上且离心率为![]() 的椭圆C相交于P、Q两点,直线y=
的椭圆C相交于P、Q两点,直线y=![]() 过线段PQ的中点,同时椭圆C上存在一点与右焦点关于直线l对称.
过线段PQ的中点,同时椭圆C上存在一点与右焦点关于直线l对称.
(1)求直线l的方程;
(2)求椭圆C的方程.
(1)设椭圆方程为 由题设知,直线l不平行于y轴,否则PQ中点在x轴上与直线y= 故可设直线l方程为y=k(x-1) ② ②代入①消y整理得:(k2a2+b2)x2-2k2a2x+a2k2-a2b2=0 ③ 设P(x1,y1),Q(x2,y2),则x1+x2= ∵ PQ的中点 ∴ 又y1+y2=k(x1+x2)-2k代入上式得: ∴ ∵ e= 故直线l的方程为y=-x+1.
(2)由(1)知,a2=2b2,方程③即为3x2-4x+2-2b2=0. 故D=16-24(1-b2)=8(3b2-1)>0,得b> 椭圆C的方程即为:x2+2y2=2b2, ④ 其右焦点为F(b,0) 设点F关于直线l的对称点为F/(x0,y0),则应有
又点在F/的椭圆上.代入④得:1+2(1-b)2=2b2.解得b= ∴ b2=
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:全优设计选修数学-2-1苏教版 苏教版 题型:013
过点(1,0)的直线与双曲线![]() =1的右支交于A、B两点,则直线AB的斜率k的取值范围是
=1的右支交于A、B两点,则直线AB的斜率k的取值范围是
|k|≥1
![]() <|k|<2
<|k|<2
|k|≤![]()
|k|<1
查看答案和解析>>
科目:高中数学 来源:江苏省泰州中学2010-2011学年高二下学期期中考试数学文科试题 题型:022
若存在过点(1,0)的直线与曲线y=x3和y=ax2+![]() x-9都相切,则a等于________.
x-9都相切,则a等于________.
查看答案和解析>>
科目:高中数学 来源:江西省六校2012届高三第一次联考数学理科试题 题型:044
已知定义在(0,+∞)上的函数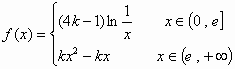 是增函数
是增函数
(1)求常数k的取值范围
(2)过点(1,0)的直线与f(x)(![]() )的图象有交点,求该直线的斜率的取值范围
)的图象有交点,求该直线的斜率的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
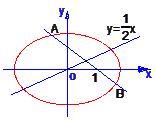
过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为![]() 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=![]() x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源:2012届湖北省高二下学期期中考试理科数学卷 题型:解答题
过点(1,0)的直线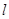 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为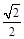 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=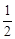 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l对称,试求直线l与椭圆C的方程
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l对称,试求直线l与椭圆C的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com