正项等比数列{an}的前n项和记为Sn,a1=1,S3=13
(Ⅰ)求{an}的通项公式;
(Ⅱ)等差数列{bn}的各项为正,且b2=5,又a1+b1,a2+b2,a3+b3成等比数列,设An=anbn,求{An}的前n项和Tn.
解:(Ⅰ)设公比为q,则S
3=1+q+q
2=13,
∴q
2+q-12=0
∴q=3或q=-4
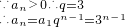
(Ⅱ)设{b
n}的公差为d,由b
2=5,可设b
1=5-d,b
3=5+d
又a
1=1,a
2=3,a
3=9,由题意可得(5-d+1)(5+d+9)=(5+3)
2,解得d
1=2,d
2=-10
∵等差数列{b
n}的各项为正,∴d>0∴d=2,∴b
1=5-d=3
∴b
n=b
1+(n-1)d=3+(n-1)×2=2n+1
∵A
n=a
nb
n=(2n+1)•3
n-1则T
n=3+5×3+7×3
2+9×3
3+…+(2n+1)3
n-1①
∴3T
n=3×3+5×3
2+7×3
3+9×3
4+…+(2n+1)3
n②
由①-②得-2T
n=3+2×(3+3
2+3
3+…+3
n-1)-(2n+1)3
n=3+2

=3-3+3
n-(2n+1)3
n=-2n•3
n∴T
n=n•3
n分析:(Ⅰ)先由a
1=1以及S
3=13求出等比数列的公比,即可得到{a
n}的通项公式;(注意是正项等比数列,公比为正).
(Ⅱ)先由条件b
2=5,以及a
1+b
1,a
2+b
2,a
3+b
3成等比数列求出等差数列{b
n}的通项公式;再利用错位相减法求出{A
n}的前n项和T
n即可.
点评:本题第二问主要涉及到错位相减法求数列和的应用问题.错位相减法求数列和适用与一等差数列与一等比数列组成的新数列.

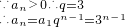
 =3-3+3n-(2n+1)3n=-2n•3n
=3-3+3n-(2n+1)3n=-2n•3n
