
【题目】已知函数f(x)=x3+3x2﹣9x+3.求:
(1)f(x)的单调递增区间;
(2)f(x)的极值.
【答案】
(1)解:f′(x)=3x2+6x﹣9,解f′(x)≥0得:
x≥1,或x≤﹣3;
∴f(x)的单调递增区间为(﹣∞,﹣3],[1,+∞);
(2)解:x<﹣3时,f′(x)>0,﹣3<x<1时,f′(x)<0,x>1时,f′(x)>0;
∴x=﹣3时f(x)取极大值30,x=1时,f(x)取极小值﹣2.
【解析】(1)可求导数得到f′(x)=3x2+6x﹣9,而通过解f′(x)≥0即可得出函数f(x)的单调递增区间;(2)根据x的取值可以判断导数符号,这样由极值的概念便可得出函数f(x)的极值.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
(1)求函数f(x)的极值;
(2)在曲线y=f(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1≠x2),使得直线AB的斜率k=f′( ![]() )?若存在,求出x1与x2的关系;若不存在,请说明理由.
)?若存在,求出x1与x2的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y∈R,有f(x+y)=f(x)f(y),f(1)=2.
(1)求f(0)的值;
(2)求证:对任意x∈R,都有f(x)>0;
(3)解不等式f(3﹣2x)>4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左顶点为
的左顶点为![]() ,且椭圆
,且椭圆![]() 与直线
与直线![]() 相切,
相切,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的动直线与椭圆
的动直线与椭圆![]() 交于
交于![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩. 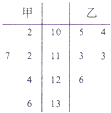
(1)从甲班的样本中有放回的随机抽取2个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名学生的成绩,记获优秀成绩的总人数为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足(an+1﹣1)(an﹣1)= ![]() (an﹣an+1),a1=2,若bn=
(an﹣an+1),a1=2,若bn= ![]() .
.
(1)证明:数列{bn}是等差数列;
(2)令cn= ![]() ,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥
,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥ ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com