
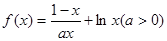
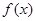 在
在 上为增函数,求实数
上为增函数,求实数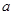 的取值范围
的取值范围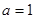 时,求
时,求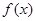 在
在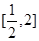 上的最大值和最小值
上的最大值和最小值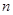 ,
,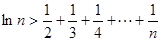 恒成立
恒成立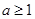 ;(2)
;(2)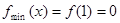 ,
,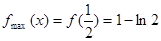 ;(3)见解析。
;(3)见解析。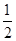 ,2]上的单调性即可
,2]上的单调性即可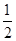 ,2]上的最大值和最小值.(3)运用第一问的结论f(x)>0,放缩法得打对
,2]上的最大值和最小值.(3)运用第一问的结论f(x)>0,放缩法得打对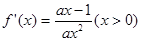 ,依题意得
,依题意得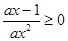 对任意
对任意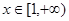 恒成立
恒成立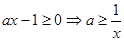 对任意
对任意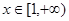 恒成立,而
恒成立,而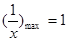
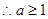
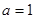 时,
时,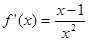 ,令
,令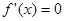 ,得
,得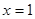 ,若
,若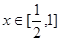 时,
时,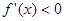 ,若
,若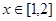 时,
时,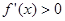 ,故
,故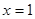 是函数在区间
是函数在区间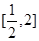 上的唯一的极小值,也是最小值,即
上的唯一的极小值,也是最小值,即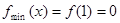 ,而
,而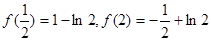 ,
, ,则
,则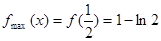
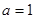 时,由(1)知
时,由(1)知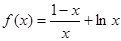 在
在 上为增函数
上为增函数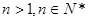 ,令
,令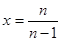 ,则
,则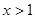 ,所以
,所以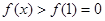
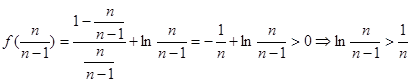
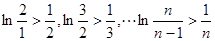
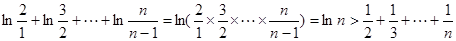


科目:高中数学 来源:不详 题型:解答题
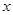 万元,每件产品的成本将降低
万元,每件产品的成本将降低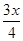 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少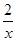 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为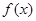 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)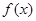 的函数解析式;
的函数解析式;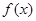 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(2,1) | B.(4,3) | C.(3,4) | D.(10,5) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
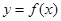 的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则
的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则 的值是
的值是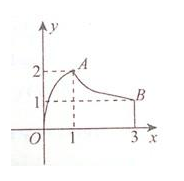
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com