
(17) 本小题考查三角函数的基本公式以及三角函数式的恒等变形等基础知识和基本运算技能.
解法一:由已知得(3sinα+2cosα)(2sinα-cosα)=0
![]() 3sinα+2cosα=0或2sinα-cosα=0.
3sinα+2cosα=0或2sinα-cosα=0.
由已知条件可知cosα≠0,所以α≠![]() ,即α∈(
,即α∈(![]() ,π).
,π).
于是tanα<0,∴tanα=-![]() .
.
sin(2α+![]() )=sin2αcos
)=sin2αcos![]() +cos2αsin
+cos2αsin![]()
=sinαcosα+![]() (cos2α-sin2α)
(cos2α-sin2α)
=![]() +
+![]() ×
×![]()
=![]() +
+![]() ×
×![]() .
.
将tanα=-![]() 代入上式得
代入上式得
sin(2α+![]() )=
)= +
+![]() ×
×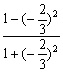
=-![]() +
+![]()
![]() ,即为所求.
,即为所求.
解法二:由已知条件可知cosα≠0,则α≠![]() ,所以原式可化为6tan2α+tanα-2=0,
,所以原式可化为6tan2α+tanα-2=0,
即(3tanα+2)(2tanα-1)=0.
又∵α∈(![]() ,π),∴tanα<0.
,π),∴tanα<0.
∴tanα=-![]() .
.
下同解法一.


科目:高中数学 来源: 题型:
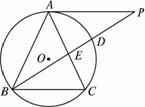
图17
A.![]() B.9 C.
B.9 C.![]() D.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com