
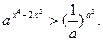
 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};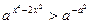 . ① ——1分
. ① ——1分
|
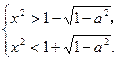 ——5分解③式得x<-
——5分解③式得x<- 或x>
或x> ,
, <x<
<x< . ——7分
. ——7分 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< }.
}. <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};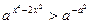 . ① ——1分
. ① ——1分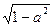 )(x2-1-
)(x2-1-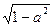 )<0. ③
)<0. ③
|
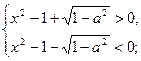
|
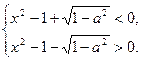 ——5分解由④、⑤组成的不等式组得
——5分解由④、⑤组成的不等式组得 <x<-
<x<- .
. <x<
<x< . ——7分
. ——7分 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
}; <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
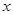 小时的收费为
小时的收费为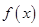 元
元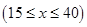 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动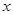 小时的收费为
小时的收费为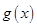 元
元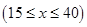 .试求
.试求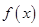 和
和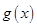 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com