
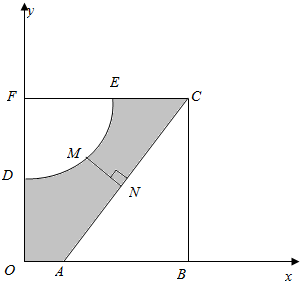
 如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.分析 (1)先求出D、E、A、C点的坐标,代入函数的解析式,从而求出a,b,k,m的值即可;
(2)①先表示出M点的坐标,问题转化为求M到直线AC的距离即可;②由基本不等式的性质求出最小值即可.
解答 解:(1)由题意得:OD=BC=4,OB=FC,
∴D(0,$\frac{7}{4}$),E(3,4),A($\frac{3}{2}$,0),C($\frac{9}{2}$,4),
把D(0,$\frac{7}{4}$),E(3,4)代入y=$\frac{x+b}{x+a}$
得:$\left\{\begin{array}{l}{\frac{b}{a}=\frac{7}{4}}\\{\frac{3+b}{3+a}=4}\end{array}\right.$,解得:a=-4,b=-7,
把A($\frac{3}{2}$,0),C($\frac{9}{2}$,4)代入y=kx+m
得:$\left\{\begin{array}{l}{\frac{3}{2}k+m=0}\\{\frac{9}{2}k+m=4}\end{array}\right.$,解得:k=$\frac{4}{3}$,m=-2;
(2)由(1)得:M点在y=$\frac{x-7}{x-4}$上,
∴M(t,$\frac{t-7}{t-4}$),t∈[0,3],
①桥MN的长l为MN到直线y=$\frac{4}{3}$x-2的距离,
故l=f(x)=$\frac{|4t-\frac{3(t-7)}{t-4}-6|}{\sqrt{{3}^{2}{+4}^{2}}}$=$\frac{1}{5}$|4t+$\frac{9}{t-4}$-9|,t∈[0,3];
②由①得:f(t)=$\frac{1}{5}$|4t+$\frac{9}{t-4}$-9|=$\frac{1}{5}$|4(t-4)+$\frac{9}{t-4}$+7|,
而t-4<0,$\frac{9}{t-4}$<0,
∴4(t-4)+$\frac{9}{t-4}$≤-2$\sqrt{4(t-4)•\frac{9}{t-4}}$=-12,
当且仅当4(t-4)=$\frac{9}{t-4}$时即t=$\frac{5}{2}$“=”成立,
∴f(t)min=$\frac{1}{5}$|-12+7|=1.
点评 本题考查了待定系数法求函数的解析式问题,考查点到直线的距离公式,考查基本不等式的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
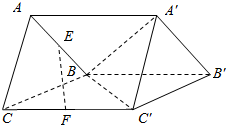 如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com