
已知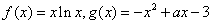 .
.
(Ⅰ)求函数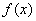 在
在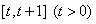 上的最小值;
上的最小值;
(Ⅱ)对一切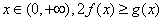 恒成立,求实数
恒成立,求实数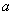 的取值范围;
的取值范围;
(Ⅲ)证明:对一切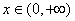 ,都有
,都有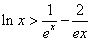 成立.
成立.
科目:高中数学 来源: 题型:
某运动某项目参赛领导小组要从甲、乙、丙、丁、戊五名志愿者中选派4人从事翻译、导游、 礼仪、司机四项不同工作,若甲、乙只能从事前三项工作,其余三人均能从事这四项工作,则不同的选派方案共有
A、18种 B、36种 C、48种 D、72种
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=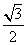 sin2x-cos2x-
sin2x-cos2x- ,x∈R.
,x∈R.
(1)求函数f(x)的最大值和最小正周期;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,且c=3,f(C)=0,若sinB=2sinA,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a=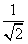 (sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
(sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
c=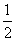 (cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
(cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
A.a>b>c B.b>a>c C.c>a>b D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
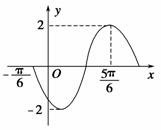
已知f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的表达式为( )
A.f(x)=2sin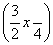 B.f(x)=2sin
B.f(x)=2sin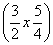
C.f(x)=2sin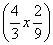 D.f(x)=2sin
D.f(x)=2sin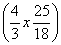
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com