已知Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,判断a2,a8,a5是否成等比数列,并说明理由.
解:由已知,S
3,S
9,S
6成等差数列,S
3+S
6=2S
9若q=1,则有S
3=3a
1,S
6=6a
1,S
9=9a
1.
即得3a
1+6a
1=18a
1,得a
1=0,不符合.∴q≠1.
∴
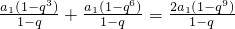
整理得q
3(2q
6-q
3-1)=0.
由q≠0得方程2q
6-q
3-1=0.(2q
3+1)(q
3-1)=0,∵q≠1,q
3-1≠0,
∴2q
3+1=0,q3=

.
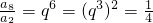
,
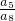
=
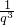
=-2,
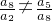
.
所以a
2,a
8,a
5不成等比数列.
分析:由已知,S
3,S
9,S
6成等差数列,既有 S
3+S
6=2S
9,分q=1,q≠1 两种情形利用等比数列前n项和公式化简S
3+S
6=2S
9得到关于q的方程,求出q的值后,再按照等比数列的定义判断a
2,a
8,a
5是否成等比数列.
点评:本题考查利用定义判断等比数列,等差数列的性质、等比数列前n项和公式,分类讨论的意识.在表示等比数列的前n项和时,务必注意公比q是否为1.

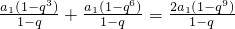
 .
.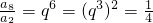 ,
,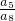 =
=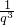 =-2,
=-2,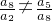 .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案