
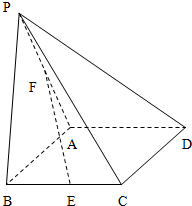
 如图,等边三角形PAB所在的平面与平行四边形ABCD所在的平面垂直,E是线段BC中点,∠ABC=60°,BC=2AB=2.
如图,等边三角形PAB所在的平面与平行四边形ABCD所在的平面垂直,E是线段BC中点,∠ABC=60°,BC=2AB=2.分析 (Ⅰ)取PD中点M,连FM,CM,推导出四边形EFMC是平行四边形,从而EF∥CM,进而EF∥平面PCD,由此得到在线段PA存在中点F,使得EF∥平面PAB.
(Ⅱ)取AB中点O,连OE并延长交DC延长线于Q,则PO⊥AB,推导出∠BAC=90°,DQ⊥OQ,PO⊥AB,从而PO⊥平面ABCD,进而DQ⊥PQ,再求出DQ⊥PO,得到∠PQO就是二面角P-CD-A的平面角,由此能求出二面角P-CD-A的余弦值.
解答 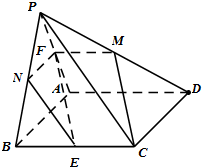 解:(Ⅰ)在线段PA存在中点F,使得EF∥平面PAB…(1分)
解:(Ⅰ)在线段PA存在中点F,使得EF∥平面PAB…(1分)
理由如下:
取PD中点M,连FM,CM.
∵F,M分别是PA,PD的中点,∴$FM∥AD,FM=\frac{1}{2}AD$,
∵平行四边形ABCD中,E是BC的中点,
∴$EC∥AD,EC=\frac{1}{2}AD$,∴EC∥FM,EC=FM,
∴四边形EFMC是平行四边形,∴EF∥CM.…(3分)
又CM?平面PCD,EF?平面PCD,∴EF∥平面PCD…(5分)
(Ⅱ)取AB中点O,连OE并延长交DC延长线于Q,则PO⊥AB
在△ABC中,∠ABC=60°,BC=2AB=2.AC2=12+22-2×1′×2×cos60°=3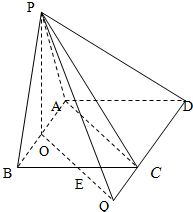 ,
,
∴AC2=AB2+BC2,∴∠BAC=90°,
又∵O,E分别是AB,BC的中点,∴OQ∥AC,OG=AC,DQ⊥OQ…(7分)
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
PO⊥AB,PO?平面PAB,∴PO⊥平面ABCD,∴DQ⊥PQ,…(8分)
又DQ⊥OQ,PO∩OQ=O,∴DQ⊥平面POQ,∴DQ⊥PO…(9分)
∴∠PQO就是二面角P-CD-A的平面角…(10分)
在等边△PAB中,$PO=\frac{{\sqrt{3}}}{2}AB=\frac{{\sqrt{3}}}{2}$,
在Rt△PQO中,$PO=\frac{{\sqrt{3}}}{2}$,$OQ=AC=\sqrt{3}$,
∴$PQ=\sqrt{O{P^2}+O{Q^2}}=\frac{{\sqrt{15}}}{2}$,$cos∠PQO=\frac{OQ}{PQ}=\frac{{2\sqrt{5}}}{5}$.…(12分)
点评 本题考查线面平行的判断,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE.
如图,四棱锥P-ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com