
把命题“若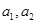 是正实数,则有
是正实数,则有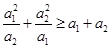 ”推广到一般情形,推广后的命题为____________.
”推广到一般情形,推广后的命题为____________.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:单选题
用反证法证明命题:“已知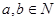 ,若
,若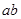 可被5整除,则
可被5整除,则 中至少有一个能被5整除”时,反设正确的是( )
中至少有一个能被5整除”时,反设正确的是( )
A. 都不能被5整除 都不能被5整除 | B. 都能被5整除 都能被5整除 |
C. 中有一个不能被5整除 中有一个不能被5整除 | D. 中有一个能被5整除 中有一个能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列说法正确的个数是 ( )
①演绎推理是由一般到特殊的推理
②演绎推理得到的结论一定是正确的
③演绎推理的一般模式是“三段论”形式
④演绎推理得到的结论的正误与大前提、小前提和推理形式有关
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列推理是归纳推理的是
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆 + + =1的面积S=πab =1的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···,第n个三角形数为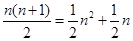 。记第n个k边形数为N(n,k)(
。记第n个k边形数为N(n,k)(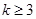 ),以下列出了部分k边形数中第n个数的表达式:
),以下列出了部分k边形数中第n个数的表达式:
三角形数 N(n,3)=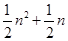
正方形数 N(n,4)=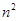
五边形数 N(n,5)=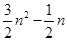
六边形数 N(n,6)=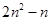
可以推测N(n,k)的表达式,由此计算N(10,24)= ____________
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
完成反证法证题的全过程.设a1,a2, ,a7是1,2, ,7的一个排列,求证:乘积p=(a1-1)(a2-2) (a7-7)为偶数.
证明:假设p为奇数,则a1-1,a2-2, ,a7-7均为奇数.因奇数个奇数之和为奇数,故有奇数= = =0.但0≠奇数,这一矛盾说明p为偶数.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线;已知直线b∥平面α,直线a?平面α,则直线b∥直线a”,结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com