
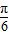 )=
)= ,则sin(2a+
,则sin(2a+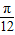 )的值为 .
)的值为 . 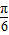 )=
)= 为正数,可得a+
为正数,可得a+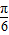 也是锐角,利用平方关系可得sin(a+
也是锐角,利用平方关系可得sin(a+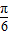 )=
)= .接下来配角,得到cosa=
.接下来配角,得到cosa=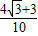 ,sina=
,sina=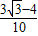 ,再用二倍角公式可得sin2a=
,再用二倍角公式可得sin2a=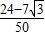 ,cos2a=
,cos2a=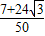 ,最后用两角和的正弦公式得到sin(2a+
,最后用两角和的正弦公式得到sin(2a+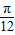 )=sin2acos
)=sin2acos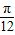 +cosasin
+cosasin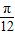 =
=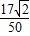 .
.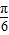 )=
)= ,
,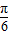 也是锐角,且sin(a+
也是锐角,且sin(a+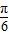 )=
)=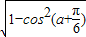 =
=
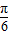 )-
)-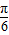 ]=
]= cos
cos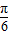 +
+ sin
sin =
=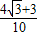
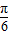 )-
)-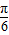 ]=
]= cos
cos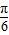 -
- sin
sin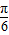 =
=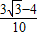
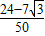 ,cos2a=cos2a-sin2a=
,cos2a=cos2a-sin2a=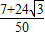
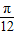 =sin(
=sin(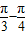 )=
)=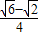 ,cos
,cos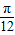 =cos(
=cos(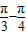 )=
)=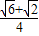
 )=sin2acos
)=sin2acos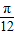 +cosasin
+cosasin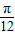 =
=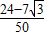 •
•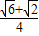 +
+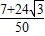 •
•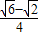 =
=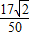
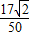
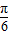 的余弦值的情况下,求2a+
的余弦值的情况下,求2a+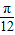 的正弦值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题.
的正弦值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题. 

 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源:2012-2013学年湖北省咸宁市四校高三(上)12月月考数学试卷(理科)(解析版) 题型:填空题
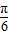 )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com