
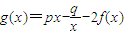 ,其中f(x)=lnx,且g(e)=
,其中f(x)=lnx,且g(e)= .(e为自然对数的底数)
.(e为自然对数的底数) (n∈N,n≥2).
(n∈N,n≥2). ,化简即可得到答案.
,化简即可得到答案.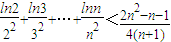 (n∈N,n≥2).因为由①知lnx≤x-1,又x>0,所以有
(n∈N,n≥2).因为由①知lnx≤x-1,又x>0,所以有 ,令x=n2,
,令x=n2,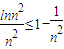 ..代入原不等式化简求解即可得到答案.
..代入原不等式化简求解即可得到答案.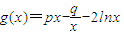 ,
,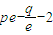 ,∴
,∴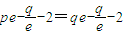 ,
,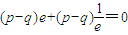 ,∴
,∴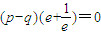 ,
,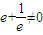 ,∴p=q
,∴p=q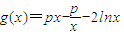 ,
,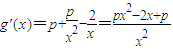 ,
,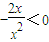 ,
,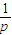 ∈(0,+∞).∴h(x)min=p-
∈(0,+∞).∴h(x)min=p-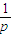 .只需p-
.只需p-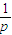 ≥0,即p≥1时h(x)≥0,g′(x)≥0,
≥0,即p≥1时h(x)≥0,g′(x)≥0, ∉(0,+∞),
∉(0,+∞),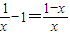 .
.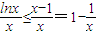 ∵n∈N*,n≥2时,令x=n2,
∵n∈N*,n≥2时,令x=n2,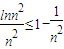 .
.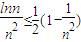 ,
,
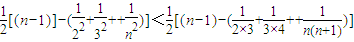
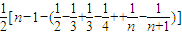
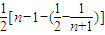 =
=


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
| x | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| a |
| b |
| b |
| c |
| a |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,其中e为自然对数的底数.
,其中e为自然对数的底数.查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=![]() (k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(l,f(l))处的切线与x轴平行.
(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(l,f(l))处的切线与x轴平行.
(Ⅰ)求k的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=xf′(x),其中f′(x)为f(x)的导函数.证明:对任意0<x<1,g(x)<1 +e-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com