
如图,过圆内接四边形 的顶点
的顶点 引圆的切线
引圆的切线 ,
, 为圆直径,若∠
为圆直径,若∠ =
= ,则∠
,则∠ =( )
=( )
A. | B. | C. | D. |
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,以坐标原点O为极点x轴的正半轴为极轴建立极坐标系, 曲线C1的极坐标方程为:
(I)求曲线C1的普通方程;
(II)曲线C2的方程为 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图, 是圆的内接三角行,
是圆的内接三角行, 的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分
的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分 ;②
;② ;③
;③ ;④
;④ .则所有正确结论的序号是( )
.则所有正确结论的序号是( )
| A.①② | B.③④ | C.①②③ | D.①②④ |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知曲线C的极坐标方程是 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 为参数)。
为参数)。
(1)写出直线 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线
得到曲线 ,设曲线
,设曲线 上任一点为
上任一点为 ,求
,求 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,圆内接四边形ABCD的一组对边AD、BC的延长线相交于点P,对角线AC、BD相交于点Q,则图中相似三角形共有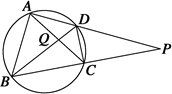
A.4对 B.2对 C.5对 D.3对
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,PA切圆于A,PA=8,直线PCB交圆于C、B,连接AB、AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则 的值等于
的值等于
A. B.
B. C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,梯形ABCD的对角线交于点O,则下列四个结论: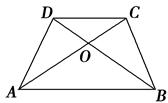
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC∶S△AOD=CD∶AB;
④S△AOD=S△BOC.
其中正确的个数为( ).
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com