
定义区间 ,
, ,
, ,
, 的长度均为
的长度均为 ,其中
,其中 .
.
(1)求关于 的不等式
的不等式 的解集构成的区间的长度;
的解集构成的区间的长度;
(2)若关于 的不等式
的不等式 的解集构成的区间的长度为
的解集构成的区间的长度为 ,求实数
,求实数 的值;
的值;
(3)已知关于 的不等式
的不等式 ,
, 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过 ,求实数
,求实数 的取值范围.
的取值范围.
(1)区间的长度是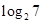 .
.
(2)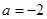 (
( 舍).
舍).
(3)实数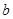 的取值范围是
的取值范围是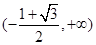 .
.
【解析】
试题分析:(1)不等式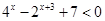 的解是
的解是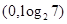
所以区间的长度是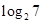 3分
3分
(2)
当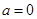 时,不符合题意 4分
时,不符合题意 4分
当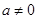 时,
时,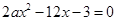 的两根设为
的两根设为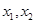 ,且
,且
结合韦达定理知 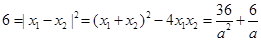
解得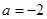 (
( 舍) 7分
舍) 7分
(3)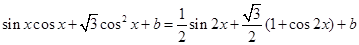
=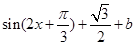
设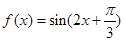 ,原不等式等价于
,原不等式等价于 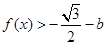 ,
, 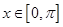 9分
9分
因为函数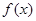 的最小正周期是
的最小正周期是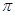 ,
,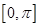 长度恰为函数的一个正周期
长度恰为函数的一个正周期
所以 时,
时,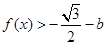 ,
, 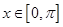 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过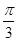
即实数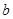 的取值范围是
的取值范围是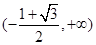 12分
12分
考点:指数不等式,和差倍半的三角函数公式,三角不等式,三角函数图象和性质。
点评:难题,指数不等式,常常化为同底数指数幂的不等关系或利用“换元法”,加以转化。三角函数不等式问题,通常利用三角公式进行化简,结合三角函数的图象和性质,加以处理,本题较难。


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| 5 |
| 6 |
| A、11 | ||
| B、6 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)+f(x1) |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com