练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=x2﹣2ax+a﹣1在区间[0，1]上有最小值﹣2，求a的值．

    【答案】解：∵函数f（x）=x2﹣2ax+a﹣1的开口向上，对称轴为x=a，
    ∴①当a≤0时，f（x）区间[0，1]上单调递增，
    ∴f（x）min=f（0）=a﹣1=﹣2，
    ∴a=﹣1；
    ②当a≥1时，f（x）区间[0，1]上单调递减，
    f（x）min=f（1）=1﹣2a+a﹣1=﹣2，
    ∴a=2；
    ③当0＜a＜1时，f（x）min=f（a）=a2﹣2a2+a﹣1=﹣2，即a2﹣a﹣1=0，
    解得a= （0，1），
    ∴a=﹣1或a=2
    【解析】利用二次函数的单调性与最值，结合题意即可求得a的值．
    【考点精析】掌握二次函数在闭区间上的最值是解答本题的根本，需要知道当时，当时，；当时在上递减，当时，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜）的图象如图所示，为了得到y=cos2x的图象，则只要将f（x）的图象（　　）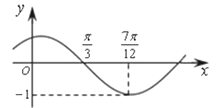

    A.向左平移个单位长度
    B.向右平移个单位长度
    C.向左平移个单位长度
    D.向右平移个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）已知a，b为正整数，a≠b，x＞0，y＞0．试比较 + 与 的大小，并指出两式相等的条件．
    （2）用（1）所得结论，求函数y= + ，x∈（0， ）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在平面直角坐标系中的一个椭圆，它的中心在原点，左焦点为F(-,0)，且过点D（2，0）．
    （1）求该椭圆的标准方程；
    （2）设点A(1,)，若P是椭圆上的动点，求线段PA的中点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， 底面， ， ， 是的中点．

    （Ⅰ）证明；

    （Ⅱ）证明平面；

    （Ⅲ）求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个焦点为，且离心率为．

    （1）求椭圆方程；

    （2）斜率为的直线过点，且与椭圆交于两点， 为直线上的一点，若△为等边三角形，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列的前项和为，公比， ， ．

    （Ⅰ）求数列{an}的通项公式；

    （Ⅱ）设， 为{}的前项和，求．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，点P到两点(0,-)，(0,)的距离之和等于4，设点P的轨迹为C．
    （1）写出C的方程；
    （2）设直线y=kx+1与C交于A、B两点，k为何值时？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司研究开发了一种新产品，生产这种新产品的年固定成本为150万元，每生产千件，需另投入成本为 (万元)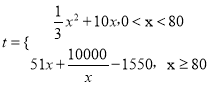， .每件产品售价为500元.该新产品在市场上供不应求可全部卖完.

    （Ⅰ）写出年利润（万元）关于年产量（千件）的函数解析式；

    （Ⅱ）当年产量为多少千件时，该公司在这一新产品的生产中所获利润最大.

    查看答案和解析>>

    同步练习册答案