【答案】
分析:(1)
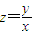
表示的是区域内的点与原点连线的斜率.故
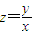
的最值问题即为直线的斜率的最大值与最小值.
(2)z=x
2+y
2的最值表示的是区域内的点与原点的两点距离的平方的最大值、最小值.
解答: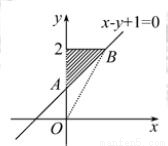
解:由
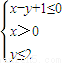
.作出可行域如图阴影部分所示:
(1)
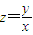
表示可行域内任一点与坐标原点连线的斜率,
因此
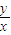
的范围为直线OB的斜率到直线OA的斜率(OA斜率不存在).
而由
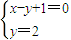
得B(1,2),∴
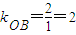
.
∴z
max不存在,z
min=2,∴z的取值范围是[2,+∞).
(2)z=x
2+y
2表示可行域内的任意一点与坐标原点的两点间距离的平方.
因此x
2+y
2的范围最小为|OA|
2(取不到),最大为|OB|
2.由
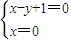
得A(0,1),
∴|OA|
2=
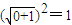
,|OB|
2=
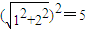
.
∴z
max=5,z无最小值.故z的取值范围是(1,5].
点评:本例与常规线性规划不同,主要是目标函数不是直线形式,此类问题常考虑目标函数的几何意义,常见代数式的几何意义主要有以下几点:
(1)
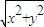
表示点(x,y)与原点(0,0)的距离;
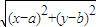
表示点(x,y)与(a,b)的距离.
(2)
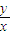
表示点(x,y)与原点(0,0)连线的斜率;
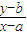
表示点(x,y)与(a,b)连线的斜率.
这些代数式的几何意义能使所求问题得以转化,往往是解决问题的关键.
(2)和或积为定值;
(3)等号能否成立,即一正、二定、三相等,这三个条件缺一不可.

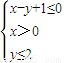 .
.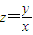 ,求z的最大值和最小值,并求z的取值范围;
,求z的最大值和最小值,并求z的取值范围;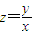 表示的是区域内的点与原点连线的斜率.故
表示的是区域内的点与原点连线的斜率.故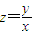 的最值问题即为直线的斜率的最大值与最小值.
的最值问题即为直线的斜率的最大值与最小值. 解:由
解:由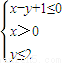 .作出可行域如图阴影部分所示:
.作出可行域如图阴影部分所示: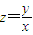 表示可行域内任一点与坐标原点连线的斜率,
表示可行域内任一点与坐标原点连线的斜率,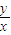 的范围为直线OB的斜率到直线OA的斜率(OA斜率不存在).
的范围为直线OB的斜率到直线OA的斜率(OA斜率不存在).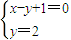 得B(1,2),∴
得B(1,2),∴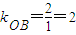 .
.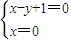 得A(0,1),
得A(0,1),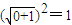 ,|OB|2=
,|OB|2=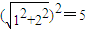 .
.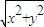 表示点(x,y)与原点(0,0)的距离;
表示点(x,y)与原点(0,0)的距离;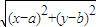 表示点(x,y)与(a,b)的距离.
表示点(x,y)与(a,b)的距离.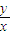 表示点(x,y)与原点(0,0)连线的斜率;
表示点(x,y)与原点(0,0)连线的斜率;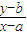 表示点(x,y)与(a,b)连线的斜率.
表示点(x,y)与(a,b)连线的斜率.
