
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候
,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候![]() 的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则
的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() ).(参考数据
).(参考数据![]() )
)
A.3.14B.3.11C.3.10D.3.05
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下述结论中错误的是( )
,则下述结论中错误的是( )
A.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 在
在![]() 有且仅有
有且仅有![]() 个极小值点
个极小值点
B.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 在
在![]() 上单调递增
上单调递增
C.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 的范围是
的范围是![]()
D.若![]() 图像关于
图像关于![]() 对称,且在
对称,且在![]() 单调,则
单调,则![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正整数数列![]() 满足:
满足:![]() ,
,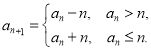
(1)写出数列![]() 的前5项;
的前5项;
(2)将数列![]() 中所有值为1的项的项数按从小到大的顺序依次排列,得到数列
中所有值为1的项的项数按从小到大的顺序依次排列,得到数列![]() ,试用
,试用![]() 表示
表示![]() (不必证明);
(不必证明);
(3)求最小的正整数![]() ,使
,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与抛物线
与抛物线![]() 有一条斜率为1的公共切线
有一条斜率为1的公共切线![]() .
.
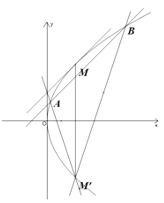
(1)求![]() .
.
(2)设![]() 与抛物线切于点
与抛物线切于点![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,在区域
,在区域![]() 内过
内过![]() 作两条关于直线
作两条关于直线![]() 对称的抛物线的弦
对称的抛物线的弦![]() ,
,![]() .连接
.连接![]() .
.
①求证:![]() ;
;
②设![]() 面积为
面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() ,
,
(1)求![]() 在
在![]() 处的切线的一般式方程;
处的切线的一般式方程;
(2)请判断![]() 与
与![]() 的图像有几个交点?
的图像有几个交点?
(3)设![]() 为函数
为函数![]() 的极值点,
的极值点,![]() 为
为![]() 与
与![]() 的图像一个交点的横坐标,且
的图像一个交点的横坐标,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,在x轴正半轴上任意选定一点
,在x轴正半轴上任意选定一点![]()
![]() ,过点M作与x轴垂直的直线交C于P,O两点.
,过点M作与x轴垂直的直线交C于P,O两点.
(1)设![]() ,证明:抛物线
,证明:抛物线![]() 在点P,Q处的切线方程的交点N与点M关于原点O对称;
在点P,Q处的切线方程的交点N与点M关于原点O对称;
(2)通过解答(1),猜想求过抛物线![]()
![]() 上一点
上一点![]() (不为原点)的切线方程的一种做法,并加以证明.
(不为原点)的切线方程的一种做法,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于各项均为正数的无穷数列![]() ,记
,记![]() ,给出下列定义:
,给出下列定义:
①若存在实数![]() ,使
,使![]() 成立,则称数列
成立,则称数列![]() 为“有上界数列”;
为“有上界数列”;
②若数列![]() 为有上界数列,且存在
为有上界数列,且存在![]() ,使
,使![]() 成立,则称数列
成立,则称数列![]() 为“有最大值数列”;
为“有最大值数列”;
③若![]() ,则称数列
,则称数列![]() 为“比减小数列”.
为“比减小数列”.
(1)根据上述定义,判断数列![]() 是何种数列?
是何种数列?
(2)若数列![]() 中,
中,![]() ,
,![]() ,求证:数列
,求证:数列![]() 既是有上界数列又是比减小数列;
既是有上界数列又是比减小数列;
(3)若数列![]() 是单调递增数列,且是有上界数列,但不是有最大值数列,求证:
是单调递增数列,且是有上界数列,但不是有最大值数列,求证:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,其左焦点为
,其左焦点为![]() .过
.过![]() 点的直线
点的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,交
两点,交![]() 轴的正半轴于点
轴的正半轴于点![]() .
.
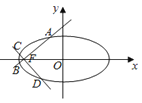
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且与
且与![]() 垂直的直线交椭圆于
垂直的直线交椭圆于![]() 、
、![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com