
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| 2 | ||
|
| 2 |
| 2 |


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
|
| π |
| 4 |
| ||
| 2 |
| ab |
| bc |
| ca |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省清远市英德一中高三(上)期末数学复习试卷(解析版) 题型:填空题
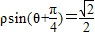 上的动点,则M、N的最小距离是 .
上的动点,则M、N的最小距离是 .查看答案和解析>>
科目:高中数学 来源:2010年广东省深圳市宝安中学高考数学考前热身训练试卷(理科)(解析版) 题型:填空题
 上的动点,则M、N的最小距离是 .
上的动点,则M、N的最小距离是 .查看答案和解析>>
科目:高中数学 来源:2010年广东省佛山市南海中学等六校高三联考数学试卷(文科)(解析版) 题型:解答题
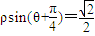 上的动点,则M、N的最小距离是 .
上的动点,则M、N的最小距离是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com