
已知圆心为(1,2)的圆C,被直线l:2x-y-5=0截得的弦长为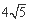 .
.
(Ⅰ)求圆C的的方程.
(Ⅱ)设P是直线l上横坐标为-4的一点,求经过点P的圆的切线方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
两圆(x-2)2+(y+3)2=13和(x-3)2+y2=9交于A,B两点,则AB的垂直平分线的方程是( )
A.x+y+3=0 B.2x-y-5=0 C.3x-y-9=0 D.4x-3y+7=0
查看答案和解析>>
科目:高中数学 来源: 题型:
在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.(-2,1)
B.(0,2)
C.(-∞,-2)∪(1,+∞)
D.(-1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系中,点P是由不等式组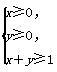 所确定的平面区域内的动点,Q是直线2x+y=0上任意一点,O为坐标原点,则|
所确定的平面区域内的动点,Q是直线2x+y=0上任意一点,O为坐标原点,则|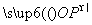 +
+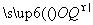 |的最小值为( )
|的最小值为( )
A.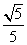 B.
B.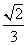 C.
C.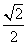 D.1
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校组织演讲比赛,准备从甲、乙等8名学生中选派4名学生参加,要求甲、乙两名同学至少有一人参加,且若甲、乙同时参加时,他们的演讲顺序不能相邻,那么不同的演讲顺序的种类为( )
A.1 860 B.1 320 C.1 140 D.1 020
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(n)=logn+1(n+2)(n∈N*),定义使f(1)·f(2)·f(3)·…·f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,2 013]内这样的企盼数共有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com