练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设f（x）=xsinx，x1、x2∈[-
    π
    2
    ，
    π
    2
    ]，且f（x1）＞f（x2），则下列结论必成立的是（　　）
    分析：由题设条件，判断出f（x）是偶函数；再利用导数的性质分别判断出函数[0，
    π
    2
    ]、[-
    π
    2
    ，0]的单调性，再用等价转化思想能求出结果．
    解答：解：∵f（x）=xsinx，
    ∴f（-x）=-xsin（-x）=xsinx=f（x），
    ∴函数f（x）=xsinx是偶函数，
    ∵f′（x）=sinx+xcosx，
    ∴x∈[0，
    π
    2
    ]    时，f′（x）≥0，f（x）是增函数，
    x∈（-
    π
    2
    ，0）时，f′（x）≤0，f（x）是减函数，
    ∵f（x1）＞f（x2），
    ∴f（|x1|）＞f（|x2|），
    ∴x1＞x2，
    ∴x12＞x22．
    故选D．
    点评：本题考查函数的奇偶性、单调性的应用，解题时要注意导数性质的合理运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f(x)=acos2ωx+
    		3
    acosωxsinωx+b(0＜ω＜2，a≠0)    ，x=
    π
    6
    是其函数图象的一条对称轴．
    （Ⅰ）求ω的值；
    （Ⅱ）若f（x）的定义域为[-
    π
    3
    ，
    π
    3
    ]    ，值域为[-1，5]，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）满足f（-x）=f（x），且当x≥0时，f(x)=(
    1
    4
    )x    ，又函数g（x）=|xsinπx|，则函数h（x）=f（x）-g（x）在[-
    1
    2
    ，2]    上的零点个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

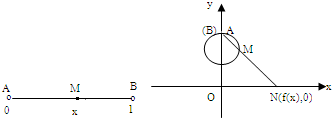    设区间（0，1）内的实数x对应数轴上的点M（如图），将线段AB围成一个圆，使两端A、B恰好重合，再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），射线AM与ox轴交于点N（f（x），0）根据这一映射法则可得f（x）与x的函数关系式为
    f（x）=
    cosπx
    sinπx
    ，x∈（0，1）
    f（x）=
    cosπx
    sinπx
    ，x∈（0，1）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知对任意平面向量
    AB
    =（x，y），我们把
    AB
    绕其起点A沿逆时针方向旋转θ角得到向量
    AP
    =（xcosθ-ysinθ，xsinθ+ycosθ），称为
    AB
    逆旋θ角到
    AP
    ．
    （1）把向量
    a
    =（2，-1）逆旋
    π
    3
    角到
    b
    ，试求向量
    b
    ．
    （2）设平面内函数y=f （x）图象上的每一点M，把
    OM
    逆旋
    π
    4
    角到
    ON
    后（O为坐标原点），得到的N点的轨迹是曲线x2-y2=3，当函数F （x）=λ f （x）-|x-1|+2有三个不同的零点时，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）满足f（﹣x）=f（x），且当x≥0时，，又函数g（x）=|xsinπx|，则函数h（x）=f（x）﹣g（x）在上的零点个数为（　　）

    　

    A．

    3

    B．

    4

    C．

    5

    D．

    6

    查看答案和解析>>

    同步练习册答案