
【题目】我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.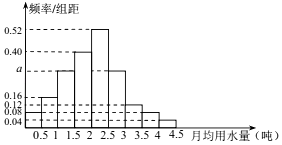
(Ⅰ)求直方图中 a 的值;
(Ⅱ)若该市政府希望使 85%的居民每月的用水量不超过标准 x(吨),估计 x 的值,并说明理由;
(Ⅲ)已知平价收费标准为 4 元/吨,议价收费标准为 8元/吨.当 x=3时,估计该市居民的月平均水费.(同一组中的数据用该组区间的中点值代替)
【答案】解:(Ⅰ)由频率分布直方图,
得:(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,
解得:a=0.30;
(Ⅱ)∵前6组的频率之和是(0.08+0.16+0.30+0.40+0.52+0.30)×0.5=0.88>0.85,
而前5组的频率之和为(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,
∴2.5≤x<3,
由0.3×(x﹣2.5)=0.85﹣0.73,解得:x=2.9,
因此,估计月用水量标准为2.9吨时,
85%的居民每月的用水量不超过标准;
(Ⅲ)设居民月用水量为t吨,相应的水费为y元,
则y= ![]() ,即y=
,即y= ![]() ,
,
由题设条件及月均用水量的频率分布直方图,
得居民每月的水费数据分组与频率分布表如下:
组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) | [10,12) | [12,16) | [16,20) | [20,24) |
频率 | 0.04 | 0.08 | 0.15 | 0.20 | 0.26 | 0.15 | 0.06 | 0.04 | 0.02 |
根据题意,该市民的月平均水费估计为:
1×0.04+3×0.08+5×0.15+7×0.20+9×0.26+11×0.15+14×0.06+18×0.04+22×0.02=8.42(元).
【解析】(I)根据频率和为1,列出方程求出a的值;(II)求出月均用水量小于2.5吨和小于3吨的百分比,计算出有85%的居民每月用水量不超过标准的值;(III)根据频率分布直方图,求出当 x=3时,估计该市居民的月平均水费.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”
B.“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件
C.若命题P:n∈N,2n>1000,则﹣P:n∈N,2n≤1000
D.命题“x∈(﹣∞,0),2x<3x”是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c
(1)若a,b,c成等比数列, ![]() ,求
,求 ![]() 的值;
的值;
(2)若A,B,C成等差数列,且b=2,设A=α,△ABC的周长为l,求l=f(α)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的两条渐近线分别为l1 , l2 , 经过右焦点F垂直于l1的直线分别交l1 , l2 于 A,B 两点.若|
的两条渐近线分别为l1 , l2 , 经过右焦点F垂直于l1的直线分别交l1 , l2 于 A,B 两点.若| ![]() |,|
|,| ![]() |,|
|,| ![]() |成等差数列,且
|成等差数列,且 ![]() 与
与 ![]() 反向,则该双曲线的离心率为( )
反向,则该双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1:(x﹣2)2+y2=16和圆O2:x2+y2=r2(0<r<2),动圆M与圆O1、圆O2都相切,切圆圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为e1 , e2(e1>e2),则e1+2e2的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来篷布发展的新机遇,2015年双11期间,某购物平台的销售业绩高达918亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品和服务全好评的次数为随机变量X: ①求对商品和服务全好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com