
����Ŀ���������ҹ�����������ҵӭ����չ���»�����2015��˫11�ڼ䣬ij����ƽ̨������ҵ���ߴ�918������ң����ͬʱ����ع��������Ƴ�����Ե��̵���Ʒ�ͷ����������ϵ���ִ�����ϵͳ��ѡ��200�γɹ����ף����������۽���ͳ�ƣ�����Ʒ�ĺ�����Ϊ0.6���Է���ĺ�����Ϊ0.75�����ж���Ʒ�ͷ������������Ľ���Ϊ80�Σ�
��1���Ƿ�����ڷ�������ʲ�����0.1%��ǰ���£���Ϊ��Ʒ�������������йأ�
��2������Ƶ����Ϊ���ʣ�ij���ڸù���ƽ̨�Ͻ��е�5�ι����У������Ʒ�ͷ���ȫ�����Ĵ���Ϊ�������X�� �������Ʒ�ͷ���ȫ�����Ĵ���X�ķֲ��У��������������ʽ��ʾ����
����X����ѧ�����ͷ��
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�� ![]() ������n=a+b+c+d��
������n=a+b+c+d��
���𰸡�
��1���⣺������ɵù�����Ʒ�ͷ������۵�2��2������Ϊ��
�Է������ | �Է������� | �ϼ� | |
����Ʒ���� | 80 | 40 | 120 |
����Ʒ������ | 70 | 10 | 80 |
�ϼ� | 150 | 50 | 200 |
����۲�ֵ ![]() ��
��
��������֪���ڷ�������ʲ�����0.1%��ǰ���£���Ϊ��Ʒ�������������йأ�
��2���⣺ÿ�ι���ʱ������Ʒ�ͷ������ĸ���Ϊ ![]() ����X��ȡֵ������0��1��2��3��4��5��
����X��ȡֵ������0��1��2��3��4��5��
���� ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
����X��B��5�� ![]() ����
����
�� ![]() ��
��
![]()
����������1���������г�2��2������������۲�ֵK2 �� �����������ɵó���ȷ�Ľ��ۣ���2���������⣬�ó���Ʒ�ͷ������ĸ��ʣ����X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д�������뷽�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�����ȱˮ�����Ϊͻ����ij������Ϊ�˹��������Լ��ˮ���ƻ��ڱ������о���������ˮ�����������ȷ��һ�������ľ�������ˮ����x���֣�����ˮ�������� x �IJ��ְ�ƽ���շѣ����� x �IJ��ְ�����շѣ�Ϊ���˽�ȫ�о�����ˮ���ķֲ������ͨ������������� 100 λ����ij����¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1��������[4��4.5]�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��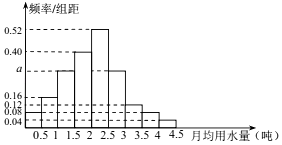
������ֱ��ͼ�� a ��ֵ��
��������������ϣ��ʹ 85%�ľ���ÿ�µ���ˮ���������� x���֣������� x ��ֵ����˵�����ɣ�
������֪ƽ���շѱ�Ϊ 4 Ԫ/�֣�����շѱ�Ϊ 8Ԫ/�֣��� x=3ʱ�����Ƹ��о������ƽ��ˮ�ѣ���ͬһ���е������ø���������е�ֵ���棩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��������ԭ�㣬������x���ϣ����ҽ���ֱ�ΪF1 �� F2 �� ��|F1F2|=2���㣨1�� ![]() ������ԲC�ϣ�
������ԲC�ϣ�
��1������ԲC�ķ��̣�
��2����F1��ֱ��l����ԲC�ཻ��A��B���㣬�ҡ�AF2B�����Ϊ ![]() ������F2ΪԲ������ֱ��l���е�Բ�ķ��̣�
������F2ΪԲ������ֱ��l���е�Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD��A1B1C1D1�У�E��F�ֱ�����AD��DD1���е㣬��AB=4�������B��E��F��ƽ��ظ����������õĽ������S���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x+m|+|2x��1|��m��R�� ��I����m=��1ʱ����ʽf��x����2�Ľ⼯��
��II�������x�IJ���ʽf��x����|2x+1|�Ľ⼯ΪA����[ ![]() ��2]A����ʵ��m��ȡֵ��Χ��
��2]A����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|+m|x+a|�� ����m=a=��1ʱ����ʽf��x����x�Ľ⼯��
������ʽf��x����2��0��m��1�������ʱ��ʵ��a��ȡֵ��Χ��{a|a�ܩ�3��a��3}����ʵ��m�ļ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Sn�ǵȱ�����{an}��ǰn��ͣ�S3 �� S9 �� S6�ɵȲ����У� ������֤��a2 �� a8 �� a5�ɵȲ����У�
�������Ȳ�����{bn}����b1=a2=1��b3=a5 �� ������{an3bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı��� ![]() Ϊ���Σ��ı���
Ϊ���Σ��ı��� ![]() Ϊƽ���ı��Σ���
Ϊƽ���ı��Σ��� ![]() ��
�� ![]() �ཻ�ڵ�
�ཻ�ڵ� ![]() ��
�� ![]() ��
��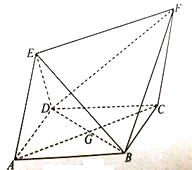
��1��֤����ƽ�� ![]() ƽ��
ƽ�� ![]() ��
��
��2���� ![]() ��������
�������� ![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲE��x2+��y�� ![]() ��2=
��2= ![]() ������ԲC��
������ԲC�� ![]() +
+ ![]() =1��a��b��0�������ҽ���F1 �� F2 �� ������ԲC�ڵ�һ���Ľ���ΪA����F1 �� E��A���㹲�ߣ�ֱ��l����ԲC��M��N���㣬��
=1��a��b��0�������ҽ���F1 �� F2 �� ������ԲC�ڵ�һ���Ľ���ΪA����F1 �� E��A���㹲�ߣ�ֱ��l����ԲC��M��N���㣬�� ![]() =��
=�� ![]() ���ˡ�0��
���ˡ�0�� 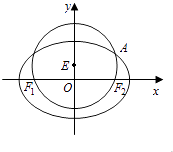
��1������ԲC�ķ��̣�
��2����������AMN�����ȡ�����ֵʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com