
【题目】已知Sn是等比数列{an}的前n项和,S3 , S9 , S6成等差数列. (Ⅰ)求证:a2 , a8 , a5成等差数列;
(Ⅱ)若等差数列{bn}满足b1=a2=1,b3=a5 , 求数列{an3bn}的前n项和Tn .
【答案】证明:(Ⅰ)设等比数列{an}的公比为q. 当q=1时,显然S3+S6≠2S9 , 与已知S3 , S9 , S6成等差数列矛盾,
∴q≠1.由S3+S6=2S9 , 可得 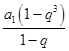 +
+  =2
=2  ,
,
化为:1+q3=2q6 , ∴a2+a5= ![]() =
= ![]() =2a8 .
=2a8 .
∴a2 , a8 , a5成等差数列.
(Ⅱ)解:由(Ⅰ)1+q3=2q6 , 解得q3=1(舍去),q3=﹣ ![]() .
.
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
b1=a2=1,b3=a5=﹣ ![]() ,
,
数列{bn}的公差d= ![]() (b3﹣b1)=﹣
(b3﹣b1)=﹣ ![]() .
.
∴bn=﹣ ![]() +
+ ![]() ,
,
故 ![]() =
= ![]() ,
,
Tn= ![]() +
+ ![]() +…+
+…+ ![]() ,①
,①![]() =
= ![]() +…+
+…+ ![]() +
+ ![]() ②
②
① ﹣②得: ![]() =﹣2+
=﹣2+ ![]()
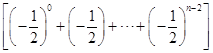 ﹣
﹣ ![]()
![]() =﹣2﹣
=﹣2﹣ 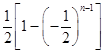 ﹣
﹣ ![]() =
= ![]() +
+ ![]()
![]() ,
,
解得Tn=﹣ ![]() +
+ ![]() .
.
【解析】(Ⅰ)设等比数列{an}的公比为q.当q=1时,显然S3+S6≠2S9 , 与已知S3 , S9 , S6成等差数列矛盾,可得q≠1.由S3+S6=2S9 , 利用求和公式化为:1+q3=2q6 , 即可证明a2 , a8 , a5成等差数列.(Ⅱ)由(Ⅰ)1+q3=2q6 , 解得q3=﹣ ![]() .可得
.可得 ![]() =
= ![]() =
= ![]() =
= ![]() .b1=a2=1,b3=a5=﹣
.b1=a2=1,b3=a5=﹣ ![]() ,可得bn=﹣
,可得bn=﹣ ![]() +
+ ![]() ,
, ![]() =
= ![]() ,再利用“错位相减法”与等比数列的求和公式即可得出.
,再利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系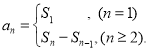 .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)ex+ax2有两个零点. (Ⅰ)求a的取值范围;
(Ⅱ)设x1 , x2是f(x)的两个零点,证明x1+x2<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来篷布发展的新机遇,2015年双11期间,某购物平台的销售业绩高达918亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品和服务全好评的次数为随机变量X: ①求对商品和服务全好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1、F2是双曲线C: ![]() =1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
A.(1,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.(1, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P( ![]() ,1)和椭圆C:
,1)和椭圆C: ![]() +
+ ![]() =1.
=1.
(1)设椭圆的两个焦点分别为F1 , F2 , 试求△PF1F2的周长及椭圆的离心率;
(2)若直线l: ![]() x﹣2y+m=0(m≠0)与椭圆C交于两个不同的点A,B,设直线PA与PB的斜率分别为k1 , k2 , 求证:k1+k2=0.
x﹣2y+m=0(m≠0)与椭圆C交于两个不同的点A,B,设直线PA与PB的斜率分别为k1 , k2 , 求证:k1+k2=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com