练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，ABCD是⊙O的内接四边形，延长BC到E；已知∠BCD∶∠ECD=3∶2，那么∠BOD等于

    [　　]

    A．120°

    B．136°

    C．144°

    D．150°
    答案：C
    解析：

    解析：由圆内接四边形性质知∠A=∠DCE，而∠BCD∶∠ECD=3∶2，且∠BCD＋∠ECD=180°，∠ECD=72°，∴∠A=72°．

    又由圆周角定理知：∠BOD=2∠A=144°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：047

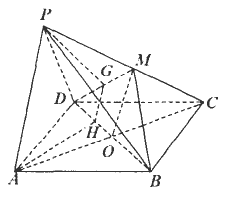
    如下图：ABCD是平行四边形，P是平面ABCD外一点，M是PC中点，在DM上取一点G，过G和AP作平面交平面DMB于CH，

    求证：AP∥GH．

    查看答案和解析>>

    科目：高中数学 来源：江苏金练·高中数学、全解全练、数学必修4 题型：022

    如下图，ABCD是边长为3的正方形，把各边三等分后，共有16个交点，从中选取2个交点组成向量，则与平行且长度为2的向量个数是________

    查看答案和解析>>

    科目：高中数学 来源：导学大课堂必修二数学苏教版 苏教版 题型：044

    如下图，ABCD是边长为3的正方形，M∈AB，N∈BC，且AM＝BN＝AB，剪掉△MNB，以DM、DN为折痕，将DA与DC重合于点P，可以构成一个无底的三棱锥，求这个三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    如下图，ABCD是直角梯形，∠ABC＝90°，SA⊥面ABCD，SA＝AB＝BC＝1，AD＝，

    (1)求面SCD与面SBA所成的二面角的正切值；

    (2)求SC与平面ABCD所成的角的余弦值．

    查看答案和解析>>

    同步练习册答案