
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
【答案】(1)an=3n-2,bn=2n;(2)(3n-4)2n+2+16.
【解析】
(1)根据题意设等差数列{an}的公差为d,等比数列{bn}的公比为q,代入已知条件计算即可.
(2)由数列{an}和{bn}的通项公式写出数列{a2nbn}的前n项和,再利用错位相减法计算即可.
解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.
由已知b2+b3=12,得b1(q+q2)=12,而b1=2
∴q2+q-6=0.
又∵q>0,解得q=2.
∴bn=2n
由b3=a4-2a1,可得3d-a1=8①
由S11=11b4,可得a1+5d=16②
联立①②,解得a1=1,d=3,由此可得an=3n-2.
∴{an}的通项公式为an=3n-2,{bn}的通项公式为bn=2n.
(2)设数列{a2nbn}的前n项和为Tn,由a2n=6n-2,有
Tn=4×2+10×22+16×23+…+(6n-2)×2n,
2Tn=4×22+10×23+16×24+…+(6n-8)×2n+(6n-2)×2n+1.
上述两式相减,得![]()
![]() .得Tn=(3n-4)2n+2+16.
.得Tn=(3n-4)2n+2+16.
∴数列{a2nbn}的前n项和为(3n-4)2n+2+16.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆锥曲线![]() (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 、
、![]() 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交此圆锥曲线于
交此圆锥曲线于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义首项为1且公比为正数的等比数列为“M-数列”.
(1)已知等比数列{an}满足:![]() ,求证:数列{an}为“M-数列”;
,求证:数列{an}为“M-数列”;
(2)已知数列{bn}满足:![]() ,其中Sn为数列{bn}的前n项和.
,其中Sn为数列{bn}的前n项和.
①求数列{bn}的通项公式;
②设m为正整数,若存在“M-数列”{cn}![]() ,对任意正整数k,当k≤m时,都有
,对任意正整数k,当k≤m时,都有![]() 成立,求m的最大值.
成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
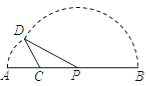
【题目】如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).求f(x)的最大值( ).
A. ![]() B. 2
B. 2
C.3 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com