练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点在抛物线上，则当点到点的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为（ ）

    A. B. C. D.

    【答案】D

    【解析】

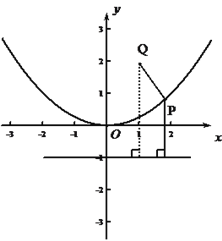
    因为点到抛物线焦点距离等于点到抛物线的准线的距离，所以到点的距离与点到抛物线焦点距离之和取得最小等价于到点的距离与点到抛物线准线距离之和取得最小，如图，由几何性质可得，从向准线作垂线，其与抛物线交点就是所求点，将代入，可得，点到点的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为，故选D.

    【方法点晴】本题主要考查抛物线的标准方程和抛物线的简单性质及利用抛物线的定义求最值，属于难题.与抛物线的定义有关的最值问题常常实现由点到点的距离与点到直线的距离的转化：(1)将抛物线上的点到准线的距化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解；(2)将拋物线上的点到焦点的距离转化为到准线的距离，利用“点与直线上所有点的连线中垂线段最短”原理解决.本题是将到焦点的距离转化为到准线的距离，再根据几何意义解题的.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在区间上任取一个数记为a，在区间上任取一个数记为b．

    若a，，求直线的斜率为的概率；

    若a，，求直线的斜率为的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，，，，点为的中点．

    （1）求证：平面；

    （2）若平面 平面，求直线与平面所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，BC= ，AB=AC=AA1=1，D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA1 ．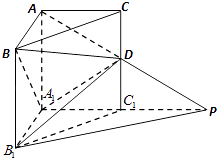

    （1）求证：CD=C1D；
    （2）求二面角A1﹣B1D﹣P的平面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆：的右焦点为，右顶点、上顶点分别为点，

    已知椭圆的焦距为，且.

    （1）求椭圆的方程；

    （2）若过点的直线交椭圆于两点，当面积取得最大时，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设点P是曲线y=x3﹣ x+ 上的任意一点，点P处的切线倾斜角为α，则α的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=﹣x2+alnx（a∈R）．
    （1）当a=2时，求函数f（x）在点（1，f（1））处的切线方程；
    （2）若函数g（x）=f（x）﹣2x+2x2 ， 讨论函数g（x）的单调性；
    （3）若（2）中函数g（x）有两个极值点x1 ， x2（x1＜x2），且不等式g（x1）≥mx2恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面是边长为的菱形, .

    （1）求证：平面平面；

    （2）若，求锐角二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆与轴相切于点，且被轴所截得的弦长为，圆心在第一象限.

    （Ⅰ）求圆的方程；

    （Ⅱ）若点是直线上的动点，过作圆的切线，切点为，当△的面积最小时，求切线的方程.

    查看答案和解析>>

    同步练习册答案