
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
| OM |
| OP |
查看答案和解析>>
科目:高中数学 来源:2013届内蒙古呼伦贝尔市高二期末考试理科数学试卷(解析版) 题型:解答题
在极坐标系中,从极点O作直线与另一直线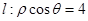 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使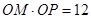 .
.
(1)求点P的轨迹方程;(2)设R为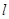 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷二文科数学 题型:填空题
(坐标系与参数方程选做题)在极坐标系中,从极点O作直线与另一直线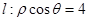 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使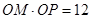 .设R为
.设R为 上任意一点,则RP的最小值 .
上任意一点,则RP的最小值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com