
(本小题满分12)如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使PD⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求平面EFG与平面PDC所成角的大小;
(3)求点A到平面EFG的距离。

解法一:(Ⅰ)如图. 以D为坐标原点,直线DA、DC、DP分别为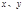 与z轴建立空间直角坐标系:
与z轴建立空间直角坐标系:
则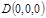
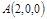
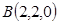
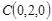
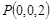
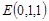
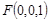
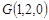
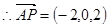
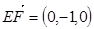
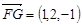
设平面GEF的法向量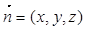 ,由法向量的定义得:
,由法向量的定义得:
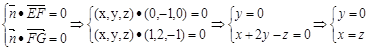
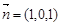 不妨设 z=1,
则
不妨设 z=1,
则
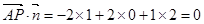
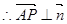 ,点P
,点P 平面EFG
平面EFG
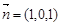 ∴AP∥平面EFG
∴AP∥平面EFG
(Ⅱ)由(Ⅰ)知平面GEF的法向量 ,
因平面EFD与坐标平面PDC重合 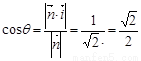 ,则它的一个法向量为
,则它的一个法向量为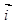 =(1,0,0)
=(1,0,0)
设平面间的夹角为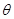 . 则
. 则
故夹角的大小为45°。
(Ⅲ)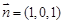 ,
,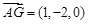
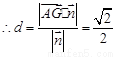
解法二:(1)∵EF∥CD∥AB,EG∥PB,根据面面平行的判定定理
∴平面EFG∥平面PAB,又PA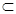 面PAB,∴AP∥平面EFG
面PAB,∴AP∥平面EFG
(2)∵平面PDC⊥平面ABCD,AD⊥DC
∴AD⊥平面PCD,而BC∥AD,∴BC⊥面EFD
过C作CR⊥EF交EF延长线于R点连GR,根据三垂线定理知
∠GRC即为二面角的平面角,∵GC=CR,∴∠GRC=45°,
故平面间的夹角大小为45°。 (3)同上
【解析】略


科目:高中数学 来源:2012-2013学年福建安溪一中、养正中学高三上学期期中联考文数学试卷(解析版) 题型:解答题
(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱.
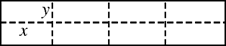
(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米时,可使总造价最低?
查看答案和解析>>
科目:高中数学 来源:2011年湖北省武汉市高二上学期期末考试数学理卷 题型:解答题
((本小题满分12分)
如图所示,正方形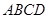 和矩形
和矩形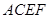 所在的平面相互垂直,已知
所在的平面相互垂直,已知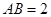 ,
,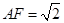 .
.
(Ⅰ)求证: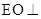 平面
平面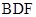 ;
;
(Ⅱ)求二面角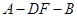 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省长沙市长望浏宁四县高三3月调研考试数学文卷 题型:解答题
(本小题满分12分)
如图,在三棱柱ADF—BCE中,侧棱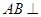 底面
底面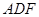 ,底面
,底面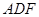 是等腰直角三角形,且
是等腰直角三角形,且 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点.
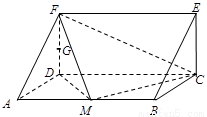
(1)求证GA∥平面FMC;
(2)求直线DM与平面ABEF所成角。
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省高一上学期12月月考考试数学 题型:解答题
.(本小题满分12分)
如图,在正方体 中,E、F分别是中点。
中,E、F分别是中点。
(Ⅰ)求证: ;
;
(Ⅱ)求证: ;
;

(III)棱 上是否存在点P使
上是否存在点P使 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2010年河北省高二下学期期末考试数学(理)试题 题型:解答题
(本小题满分12分)
如图,在正三棱柱 .
.
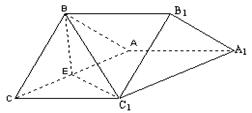
(I)若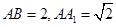 ,求点
,求点 到平面
到平面 的距离;
的距离;
(Ⅱ)当 为何值时,二面角
为何值时,二面角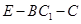 的正弦值为
的正弦值为 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com