
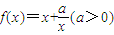 ,直线l:y=x,在曲线C上有一个动点P,过点P分别作直线l和y轴的垂线,垂足分别为A,B.再过点P作曲线C的切线,分别与直线l和y轴相交于点M,N,O是坐标原点.若△ABP的面积为
,直线l:y=x,在曲线C上有一个动点P,过点P分别作直线l和y轴的垂线,垂足分别为A,B.再过点P作曲线C的切线,分别与直线l和y轴相交于点M,N,O是坐标原点.若△ABP的面积为 ,则△OMN的面积为 .
,则△OMN的面积为 . 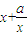 ),则B(0,
),则B(0,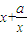 ),
),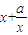 )=-(x-x)
)=-(x-x)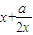 ,故点A(
,故点A(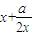 ,
,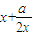 ),
),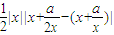
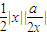 =
=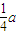 =
= ,解得a=2,
,解得a=2,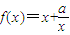 ,所以
,所以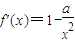 ,故切线率为
,故切线率为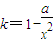 ,
,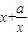 )=(
)=(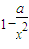 )(x-x),
)(x-x),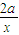 ,故点N(0,
,故点N(0,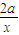 ),
),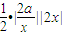 =2a=4,
=2a=4,

科目:高中数学 来源:2010-2011学年西藏拉萨中学高三第七次月考考试文科数学 题型:选择题
已知曲线C: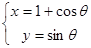 ,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
A.b= B.b=-
B.b=- C.b=5
D.b=
C.b=5
D.b= 或b=-
或b=-
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省盐城中学高二(下)期末数学试卷(理科)(解析版) 题型:解答题
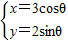 ,直线l:ρ(cosθ-2sinθ)=12.
,直线l:ρ(cosθ-2sinθ)=12.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州中学高三(上)12月质量检测数学试卷(解析版) 题型:解答题
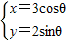 ,直线l:ρ(cosθ-2sinθ)=12.
,直线l:ρ(cosθ-2sinθ)=12.查看答案和解析>>
科目:高中数学 来源:2010年高考数学调研试卷(解析版) 题型:解答题
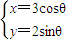 ,直线l:ρ(cosθ-2sinθ)=12.
,直线l:ρ(cosθ-2sinθ)=12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com