
设定点M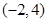 ,动点N在圆
,动点N在圆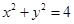 上运动,线段MN的
上运动,线段MN的
中点为点P.
(1)求MN的中点P的轨迹方程;
(2)直线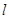 与点P的轨迹相切,且
与点P的轨迹相切,且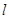 在
在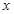 轴.
轴.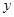 轴上的截距相等,求直线
轴上的截距相等,求直线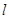 的方程.
的方程.
解:(1)设P点坐标为(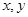 ),N点坐标为(
),N点坐标为(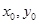 ),则由中点坐标公式有
),则由中点坐标公式有
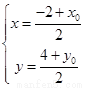
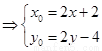
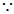 N点在圆
N点在圆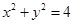 上
上
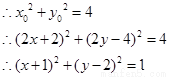
即为点P的轨迹方程 …………………6分
(2)因直线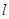 在
在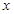 轴、
轴、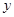 轴上截距相等,故
轴上截距相等,故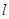 的斜率存在且不为0,当直线
的斜率存在且不为0,当直线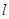 在
在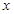 轴、
轴、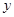 轴
轴
截距都为0时,设直线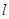 的方程为
的方程为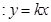
即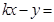 0
0
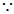 直线
直线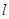 与
与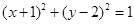 相切
相切
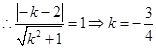 ………………9分
………………9分
当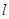 在
在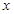 轴、
轴、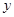 轴上的截距均不为0时,设直线
轴上的截距均不为0时,设直线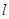 的方程为
的方程为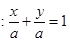
即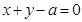
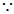 直线
直线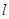 与
与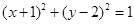 相切
相切
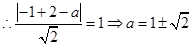 ,
,
故直线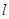 的方程为
的方程为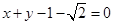 或
或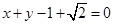
综上可知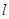 的方程为:
的方程为: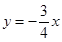
或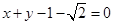 或
或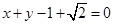 …………………12分
…………………12分
【解析】本试题主要是考查了利用相关点法求解轨迹方程,以及利用直线与圆相切的,饿到参数的值,并利用直线在两坐标轴上截距相等得到直线的方程。
(1)设P点坐标为(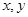 ),N点坐标为(
),N点坐标为(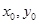 ),则由中点坐标公式有
),则由中点坐标公式有
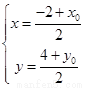
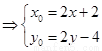
,用未知点表示已知点,代入已知关系式中得到结论。
(2)因直线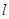 在
在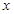 轴、
轴、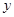 轴上截距相等,故
轴上截距相等,故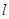 的斜率存在且不为0,当直线
的斜率存在且不为0,当直线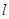 在
在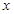 轴、
轴、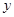 轴
轴
截距都为0时,设直线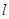 的方程为
的方程为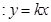
,并结合线圆相切得到斜率k的值,进而得到结论。


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 9 |
| 5 |
| 12 |
| 5 |
| 21 |
| 5 |
| 28 |
| 5 |
| 9 |
| 5 |
| 12 |
| 5 |
| 21 |
| 5 |
| 28 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com