
分析 (1)a=0时,求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,通过讨论a的范围,确定函数的单调区间,从而求出函数的最大值即可.
解答 解:(1)$a=0,f(x)=2lnx-x,f'(x)=\frac{2}{x}-1=\frac{2-x}{x}({x>0})$,
在区间(0,2)上,f'(x)>0;在区间(2,+∞)上f'(x)<0,
故f(x)的单调递增区间是(0,2),单调递减区间是(2,+∞).
(2)$f'(x)=ax-({2a+1})+\frac{2}{x}({x>0})$,$f'(x)=\frac{{({ax-1})({x-2})}}{x}({x>0})$,
①当a=0时,由(1)知f(x)在(0,2]上单调递增,
故在(0,2]上f(x)max=f(2)=2ln2-2,
②当$0<a≤\frac{1}{2}$时,$\frac{1}{a}≥2$,在区间(0,2)上,f'(x)>0;
故f(x)在(0,2]上单调递增,
故在(0,2]上f(x)max=f(2)=2ln2-2a-2,
③当$a>\frac{1}{2}$时,$0<\frac{1}{a}<2$,在区间$({0,\frac{1}{a}})$上,f'(x)>0;
在区间$({\frac{1}{a},2})$上,f'(x)<0,
f(x)在$({0,\frac{1}{a}}]$上单调递增,在$[{\frac{1}{a},2}]$上单调递减,
故在(0,2]上$f{(x)_{max}}=f({\frac{1}{a}})=-2-\frac{1}{2a}-2lna$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{11π}{12}$,0)∈A | B. | (-$\frac{7π}{12}$,1)∉A | ||
| C. | {(-$\frac{7π}{12}$,1),($\frac{17π}{12}$,1)}⊆A | D. | {($\frac{π}{2}$,1),($\frac{17π}{12}$,1)}⊆A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
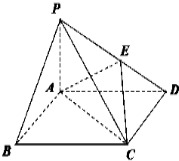 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=2,AD=4,E为线段PD上一点,且$\frac{PE}{PD}$=$\frac{1}{2}$.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB=2,AD=4,E为线段PD上一点,且$\frac{PE}{PD}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com