
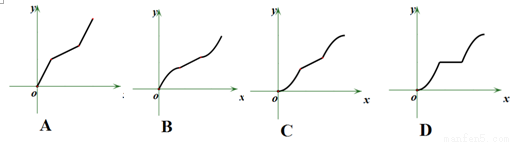
如图,不规则四边形ABCD中:AB和CD 是线段,AD和BC是圆弧,直线l⊥AB与E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,则左侧部分面积y 是关于x的函数,其大致图象为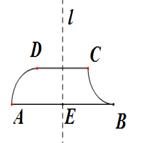
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 (2012•包头一模)如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,DE=1,BC=2,又AC=1,∠ACB=120°,CD⊥AB,直线AE与直线CD所成角为60°.
(2012•包头一模)如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,DE=1,BC=2,又AC=1,∠ACB=120°,CD⊥AB,直线AE与直线CD所成角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•河南模拟)选修4-1:几何证明选讲
(2012•河南模拟)选修4-1:几何证明选讲查看答案和解析>>
科目:高中数学 来源: 题型:
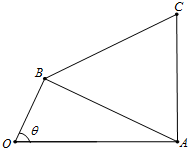 如图,四边形OACB中,a,b,c△ABC的内角A,B,C的对边,且满足sinB+sinC=2sin(B+C).
如图,四边形OACB中,a,b,c△ABC的内角A,B,C的对边,且满足sinB+sinC=2sin(B+C).查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省高三上学期期末联考文科数学试卷(解析版) 题型:选择题
如图,不规则四边形ABCD中:AB和CD 是线段,AD和BC是圆弧,直线l⊥AB于E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,左侧部分面积为y,则y关于x的大致图象为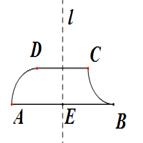

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com