已知数列{an}满足:a1=1,a2=2,且an+2=(2+cosnπ)(an-1)+3,n∈N*.
(1)求通项公式an;
(2)设{an}的前n项和为Sn,问:是否存在正整数m、n,使得S2n=mS2n-1?若存在,请求出所有的符合条件的正整数对(m,n),若不存在,请说明理由.
【答案】
分析:(1)确定a
1,a
3,…,a
2n-1,…是首项为1,公差为2的等差数列;a
2,a
4,…,a
2n,…是首项为2,公比为3的等比数列,从而可得通项公式a
n;
(2)由(1)先求出S
2n,S
2n-1的表达式,若存在正整数m、n,使得S
2n=mS
2n-1,则m=
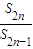
≤3,再分类讨论,即可求得结论.
解答:解:(1)当n是奇数时,cosnπ=-1;当n是偶数时,cosnπ=1.
所以,当n是奇数时,a
n+2=a
n+2;当n是偶数时,a
n+2=3a
n. …(2分)
又a
1=1,a
2=2,,所以a
1,a
3,…,a
2n-1,…是首项为1,公差为2的等差数列;
a
2,a
4,…,a
2n,…是首项为2,公比为3的等比数列. …(4分)
所以,a
n=
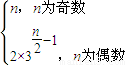
. …(6分)
(2)由(1),得S
2n=(a
1+a
3+…+a
2n-1)+(a
2+a
4+…+a
2n)=3
n+n
2-1,
S
2n-1=S
2n-a
2n=3
n+n
2-1-2×3
n-1=3
n-1+n
2-1. …(8分)
所以,若存在正整数m、n,使得S
2n=mS
2n-1,则m=
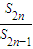
=1+
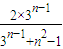
≤1+
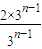
=3. …(9分)
显然,当m=1时,S
2n=3
n+n
2-1≠1×3
n-1+n
2-1=S
2n-1;
当m=2时,由S
2n=2S
2n-1,整理得3
n-1=n
2-1.
显然,当n=1时,3
1-1≠1
2-1;
当n=2时,3
2-1=2
2-1,
所以(2,2)是符合条件的一个解. …(11分)
当n≥3时,
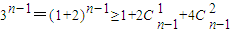
=2n
2-4n+3=(n-2)
2+n
2-1>n
2-1. …(12分)
当m=3时,由S
2n=3S
2n-1,整理得n=1,
所以(3,1)是符合条件的另一个解.
综上所述,所有的符合条件的正整数对(m,n),有且仅有(3,1)和(2,2)两对. …(14分)
点评:本题考查数列的通项,考查存在性问题的探究,考查分类讨论的数学思想,属于中档题.

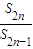 ≤3,再分类讨论,即可求得结论.
≤3,再分类讨论,即可求得结论.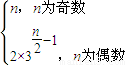 . …(6分)
. …(6分)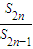 =1+
=1+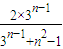 ≤1+
≤1+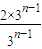 =3. …(9分)
=3. …(9分)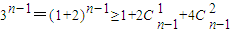 =2n2-4n+3=(n-2)2+n2-1>n2-1. …(12分)
=2n2-4n+3=(n-2)2+n2-1>n2-1. …(12分)

 阅读快车系列答案
阅读快车系列答案