已知f(x)的定义域是x≠0的一切实数,对于定义域内任意的x1,x2都有f(x1•x2)=f(x1)+f(x2),且当x>1时,f(x)>0,f(2)=1.
(1)求证f(x)是偶函数;
(2)求证f(x)在(0,+∞)上是增函数;
(3)若f(a+1)>f(a)+1,求实数a的取值范围.
解:(1)由题意知,对定义域内的任意x
1,x
2都有f(x
1•x
2)=f(x
1)+f(x
2),
令x
1=x
2=1,代入上式解得f(1)=f(1)+f(1)∴f(1)=0
令x
1=x
2=-1,代入上式解得f(1)=f(-1)+f(-1)=0∴f(-1)=0,
令x
1=-1,x
2=x代入上式,∴f(-x)=f(-1•x)=f(-1)+f(x)=f(x),
∴f(x)是偶函数.
(2)设x
2>x
1>0,则
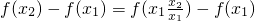
=
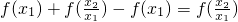
∵x
2>x
1>0,∴

,∴
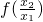
>0,
即f(x
2)-f(x
1)>0,∴f(x
2)>f(x
1)
∴f(x)在(0,+∞)上是增函数.
(3)∵f(2)=1
∴f(a+1)>f(a)+1=f(a)+f(2)=f(2a)
∵f(x)是偶函数;
∴f(|x|)=f(-x)=f(x)则f(a+1)>f(2a)即f(|a+1|)>f(|2a|)
∵f(x)在(0,+∞)上是增函数.
∴|a+1|>|2a|
两边平方得a
2+2a+1>4a
2
即3a
2-2a-1<0解得-

<a<1
分析:(1)根据题意和式子的特点,先令x
1=x
2=1,求出f(1)=0,令x
1=x
2=-1求出f(-1)=0,再令x
1=-1,x
2=x求出f(-x)=f(x),则证出此函数为偶函数;
(2)先任取x
2>x
1>0,再代入所给的式子进行作差变形,利用x
2=
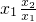
和

且
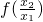
>0,判断符号并得出结论;
(3)根据f(2)=1得f(a+1)>f(a)+1=f(a)+f(2)=f(2a),然后根据偶函数f(x)得f(|a+1|)>f(|2a|),最后根据f(x)在(0,+∞)上是增函数建立不等关系,解之即可.
点评:本题主要考查了抽象函数及其应用,以及函数的奇偶性和单调性,同时考查了不等式的解法,属于中档题.

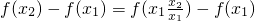 =
=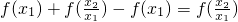
 ,∴
,∴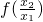 >0,
>0, <a<1
<a<1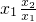 和
和 且
且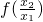 >0,判断符号并得出结论;
>0,判断符号并得出结论;
