
分析 (1)利用对数性质、运算法则、换底公式求解.
(2)利用指数性质、运算法则求解.
解答 (本小题满分12分)
解:(1)$2{log_3}2-{log_3}\frac{32}{9}+{log_3}8-{5^{{{log}_5}3}}$
=2$lo{g}_{3}2-(lo{g}_{3}32-lo{g}_{3}9)+lo{g}_{3}{2}^{3}-{5}^{lo{g}_{5}3}$
=2log32-(5log32-2log33)+3log32-3
=-3log32+2+3log32-3
=-1.(6分)
(2)${0.064^{-\frac{1}{3}}}-{({-\frac{1}{8}})^0}+{16^{\frac{3}{4}}}+{0.25^{\frac{1}{2}}}+2{log_3}6-{log_3}12$
=[(0.4)3]-${\;}^{\frac{1}{3}}$-1+(24)${\;}^{\frac{3}{4}}$+0.5+log336-log312
=(0.4)-1-1+8+0.5+log33
=2.5-1+8+0.5+1=11.(12分)
点评 本题考查对数式、指数式化简求值,是基础题,解题时要认真审题,注意对数、指数性质、运算法则、换底公式的合理运用.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:解答题
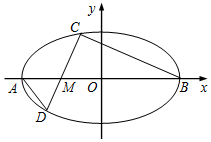 在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,两个顶点分别为A(-a,0),B(a,0),点M(-1,0),且3$\overrightarrow{AM}$=$\overrightarrow{MB}$,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.
在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,两个顶点分别为A(-a,0),B(a,0),点M(-1,0),且3$\overrightarrow{AM}$=$\overrightarrow{MB}$,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
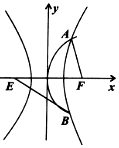 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于不同的两点A,B,若$|AF|=\frac{4}{5}|BE|$,则双曲线的离心率为$4±\sqrt{7}$.
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于不同的两点A,B,若$|AF|=\frac{4}{5}|BE|$,则双曲线的离心率为$4±\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-5y-11=0 | B. | 5x-3y-13=0 | C. | 5x+3y-7=0 | D. | 3x+5y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{6}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f ( x )=1-x | B. | f ( x )=x | C. | f ( x )=0 | D. | f ( x )=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com