
分析 若命题p正确,则△>0,解得m范围.若命题q正确,则△<0,解得m范围.若“p∨q”为真,“p∧q”为假,则p与q必然一真一假,即可得出答案.
解答 解:命题p:方程x2+2mx+1=0有两个不相等的实根,
∴△=4m2-4>0,解得m>1或m<-1.
命题q:方程x2+2(m-2)x-3m+10=0无实根,
∴△=4(m-2)2-4(10-3m)<0,解得-2<m<3.
若“p∨q”为真,“p∧q”为假,
则p与q必然一真一假,
∴p真q假时,m≥3或m≤-2.
p假q真时,-1≤m≤1.
∴实数m的取值范围是m≤-2,或-1≤m≤1,或m≥3
点评 本题以命题的真假判断与应用为载体,考查了一元二次方程的实数根与判别式的关系、一元二次不等式的解与判别式的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-16]∪[2,+∞) | B. | (-16,2) | C. | [2,+∞) | D. | (-∞,-16] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1:$\sqrt{3}$ | B. | 2:2:$\sqrt{3}$ | C. | 1:1:2 | D. | 1:1:4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
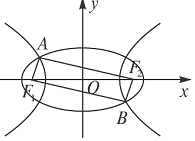 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )| A. | $y=±\sqrt{2}x$ | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{\sqrt{6}}}{2}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com