
(本小题满分10分)如图,在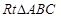 中,
中,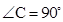 ,
,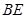 平分
平分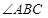 交
交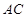 于点
于点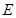 ,点
,点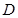 在
在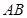 上,
上,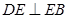 .
.

(1)求证: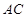 是△
是△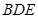 的外接圆的切线;
的外接圆的切线;
(2)若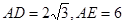 ,求
,求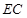 的长.
的长.
(1)见解析;(2)EC=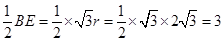 .
.
【解析】本试题主要是考查了角平分线的性质,以及直线与圆的位置关系的运用。利用线线平行的判定定理得到平行的判定,并运用勾股定理得到结论。
解(1)取BD的中点O,连接OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.又∵OB=OE,∴∠OBE=∠BEO,
∴∠CBE=∠BEO,∴BC∥OE.………………3分
∵∠C=90°,∴OE⊥AC,∴AC是△BDE的外接圆的切线. 5分
(2)设⊙O的半径为r,则在△AOE中,
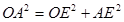 ,即
,即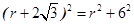 解得
解得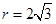 , 7分
, 7分
∴OA=2OE,∴∠A=30°,∠AOE=60°.∴∠CBE=∠OBE=30°.
∴EC=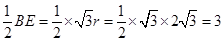 .…………10分
.…………10分


科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com