
给出下列四个命题:
①函数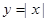 与函数
与函数 表示同一个函数;
表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数 的图像可由
的图像可由 的图像向上平移1个单位得到;
的图像向上平移1个单位得到;
④若函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 ;
;
⑤设函数 是在区间
是在区间 上图象连续的函数,且
上图象连续的函数,且 ,则方程
,则方程 在区间
在区间 上至少有一实根;
上至少有一实根;
其中正确命题的序号是 .(填上所有正确命题的序号)
③⑤
【解析】
试题分析:①因为函数 的定义域为R,函数
的定义域为R,函数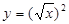 的定义域为
的定义域为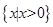 ,所以函数
,所以函数 与函数
与函数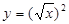 不表示同一个函数;
不表示同一个函数;
②奇函数的图像一定通过直角坐标系的原点,此命题错误,若奇函数在x=0处没定义,则奇函数的图像就不过原点;
③函数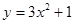 的图像可由
的图像可由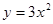 的图像向上平移1个单位得到;,正确。
的图像向上平移1个单位得到;,正确。
④因为函数 的定义域为
的定义域为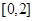 ,所以
,所以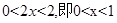 ,所以函数
,所以函数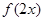 的定义域为
的定义域为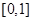 ;
;
⑤设函数 是在区间
是在区间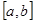 上图象连续的函数,且
上图象连续的函数,且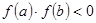 ,则方程
,则方程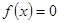 在区间
在区间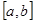 上至少有一实根,正确。
上至少有一实根,正确。
考点:函数的定义;奇函数的性质;图像的变换;抽象函数的定义域;函数零点存在性定理。
点评:此题考查的知识点较多,较为综合,属于中档题。抽象函数的有关问题对同学们来说具有一定的难度,特别是求函数的定义域,很多同学解答起来总感棘手,鉴于此,我们在学习时要善于总结。①已知 的定义域求
的定义域求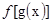 的定义域,其解法是:若
的定义域,其解法是:若 的定义域为
的定义域为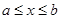 ,则在
,则在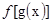 中,
中,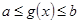 ,从中解得x的取值范围即为
,从中解得x的取值范围即为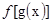 的定义域;②已知
的定义域;②已知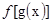 的定义域,求
的定义域,求 的定义域, 其解法是:若
的定义域, 其解法是:若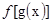 的定义域为
的定义域为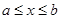 ,则由
,则由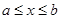 确定的
确定的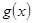 的范围即为
的范围即为 的定义域。
的定义域。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| y-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 12 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| (1+2x)2 |
| x•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com