
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 通过建立直角坐标系,利用向量的坐标运算和数量积运算及其夹角公式即可得出.
解答 解:由题意:$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则OA⊥OB,建立直角坐标系: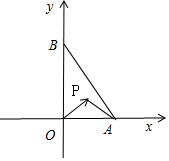 A(1,0),B(0,$\sqrt{2}$),P(x,y).
A(1,0),B(0,$\sqrt{2}$),P(x,y).
∵$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,
∴(x,y)=m(1,0)+n(0,$\sqrt{2}$)=(m,$\sqrt{2}$n),
∴x=m,y=$\sqrt{2}$n.
∵∠AOP=45°,∴cos45°=$\frac{\overrightarrow{OP}•\overrightarrow{OA}}{|\overrightarrow{OP}|•|OA|}$=$\frac{m}{\sqrt{{m}^{2}+2{n}^{2}}}$=$\sqrt{\frac{{m}^{2}}{{m}^{2}+2{n}^{2}}}$,
解得:m2=2n2
∴$\frac{n}{m}$=$\frac{\sqrt{2}}{2}$,
故选B.
点评 熟练掌握向量的坐标运算和数量积运算及其夹角公式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的顶点B到左焦点F1的距离为2,离心率e=$\frac{{\sqrt{3}}}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的顶点B到左焦点F1的距离为2,离心率e=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,+∞) | D. | (0,$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(log3π)>f(log2$\sqrt{3}$)>f(log3$\sqrt{2}$) | B. | f(log2$\sqrt{3}$)>f(log3$\sqrt{2}$)>f(log3π) | ||
| C. | f(log3$\sqrt{2}$)>f(log2$\sqrt{3}$)>f(log3π) | D. | f(log2$\sqrt{3}$)>f(log3π)>f(log3$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com