
���� ��1������֪�С�PF1F2�Ǹ�Ϊ$\sqrt{3}$�ĵȱ������Σ����a��bֵ���ɵ���ԲC�ķ���
��2�������M��N����ĺ����꣬�������ݡ�OKM=��ONK���ɵ�|OK|2=|OM|•|ON|�������ɵõ�K�����꣮
��� 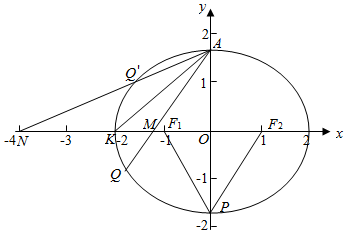 �⣺��1���ߡ�PF1F2�Ǹ�Ϊ$\sqrt{3}$�ĵȱ������Σ�
�⣺��1���ߡ�PF1F2�Ǹ�Ϊ$\sqrt{3}$�ĵȱ������Σ�
��a=2c=2��b=$\sqrt{3}$��
��a2=4��b2=3��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1��
��2����M��x1��0����N��x2��0����
��Q��A��M���㹲�ߵã�$\frac{-\sqrt{3}}{{x}_{1}}=\frac{n-\sqrt{3}}{m}$��
��x1=$\frac{-\sqrt{3}m}{n-\sqrt{3}}$��
ͬ����Q�䣬A��N���㹲�ߵã�x2=$\frac{\sqrt{3}m}{n+\sqrt{3}}$
����OKM=��ONK����tan��OKM=tan��ONK��
��$\frac{\left|OM\right|}{\left|OK\right|}=\frac{\left|OK\right|}{\left|ON\right|}$����|OK|2=|OM|•|ON|��
�֡�-$\sqrt{3}$��n��$\sqrt{3}$����n��0��
��t2=|$\frac{-\sqrt{3}m}{n-\sqrt{3}}$|•|$\frac{\sqrt{3}m}{n+\sqrt{3}}$|=$\frac{3{m}^{2}}{3-{n}^{2}}$��
�֡߶���Q����ԲC�ϣ�
��3m2+4n2=12��
��t2=$\frac{{12-4n}^{2}}{3-{n}^{2}}$=4��
��ã�t=��2��
��K��������0��-2������0��2��
���� ���⿼���֪ʶ������Բ�ı����̣�ֱ������Բ��λ�ù�ϵ���Ѷ��е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5+2$\sqrt{2}$ | B�� | 4+2$\sqrt{2}$ | C�� | $\sqrt{7}$ | D�� | 3+2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 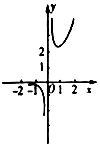 | C�� | 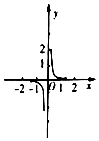 | D�� | 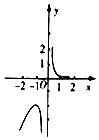 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $-\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $-\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com